Échantillonnez à partir d'un processus de Poisson

Un processus de Poisson est une généralisation du processus de Poisson unidimensionnel à un cas multidimensionnel. Un processus de Poisson homogène dans les régions géométriques peut être échantillonné en utilisant RandomPoint.

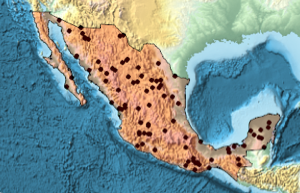
Créez un polygone des pays.

In[1]:=

region = DiscretizeGraphics[CountryData["Mexico", "Polygon"], ImageSize -> Medium]

Out[1]=

Définissez une fonction qui effectue l'échantillonnage du processus de Poisson avec trois arguments : la région, l'intensité et le nombre de réalisations.

In[2]:=

ppp[region_, intensity_, n_] := Module[{nlist, pts}, nlist = RandomVariate[PoissonDistribution[intensity RegionMeasure[region]], n]; pts = RandomPoint[region, Total[nlist]]; nlist = Accumulate[nlist]; nlist = Transpose[{Prepend[Most[nlist] + 1, 1], nlist}]; Table[Take[pts, ind], {ind, nlist}] ]

Générez une réalisation du processus de Poisson dans le polygone des pays avec une intensité de 0,5 et visualisez-la avec Graphics.

In[3]:=

intensity = 0.5; sample = ppp[region, intensity, 1];

In[4]:=

Show[region, Graphics[{Black, Point @@ sample}]]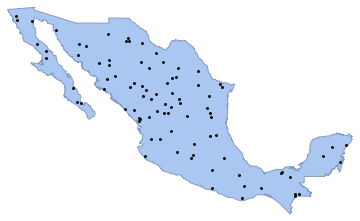

Out[4]=

Générez 10⁴ échantillons provenant du même processus. Le nombre total de points dans chaque échantillon satisfait PoissonDistribution, avec une moyenne égale à l'intensité multipliée par la superficie de la région.

In[5]:=

samples = ppp[region, intensity, 10^4]; counts = Length /@ samples;

In[6]:=

htd = PearsonChiSquareTest[counts, PoissonDistribution[intensity RegionMeasure[region]], "HypothesisTestData"];

In[7]:=

htd["TestDataTable"]

Out[7]=

In[8]:=

htd["TestConclusion"]

Out[8]=

Le nombre de points dans une sous-région est également distribué selon une loi de Poisson. Cette loi est examinée ici à l'aide d'un disque situé à l'intérieur du polygone, et le nombre de points qu'il contient est compté.

In[9]:=

disk1 = Disk[{-107, 28}, 1.5]; Show[region, Graphics[{Red, disk1}]]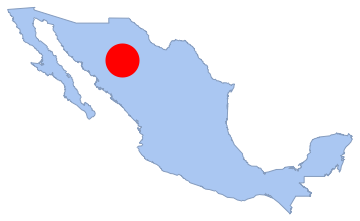

Out[9]=

In[10]:=

memberfun1 = RegionMember[disk1]; counts1 = Table[Total[Boole[memberfun1[pts]]], {pts, samples}];

Effectuez PearsonChiSquareTest sur le nombre avec une loi de Poisson.

In[11]:=

htd = PearsonChiSquareTest[counts1, PoissonDistribution[intensity RegionMeasure[disk1]], "HypothesisTestData"];

In[12]:=

htd["TestDataTable"]

Out[12]=

In[13]:=

htd["TestConclusion"]

Out[13]=

Le nombre de points dans toutes les sous-régions disjointes est indépendant. Ici, le nombre de points dans deux disques disjoints est compté et le SpearmanRankTest est effectué.

In[14]:=

disk2 = Disk[{-100, 20}, 1.3]; Show[region, Graphics[{Red, disk1, Blue, disk2}]]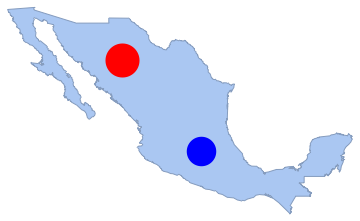

Out[14]=

In[15]:=

memberfun2 = RegionMember[disk2]; counts2 = Table[Total[Boole[memberfun2[pts]]], {pts, samples}];

In[16]:=

htd = SpearmanRankTest[counts1, counts2, "HypothesisTestData"];

In[17]:=

htd["TestDataTable"]

Out[17]=

In[18]:=

htd["TestConclusion"]

Out[18]=