Processus de Poisson inhomogène

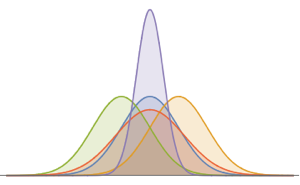
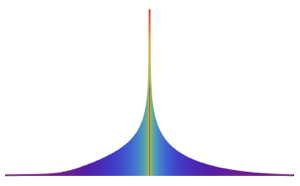
Un processus de Poisson inhomogène est un processus de Poisson avec un taux variable dans le temps. Il peut être utilisé pour modéliser les temps d'arrivée des clients dans un magasin, les événements de la circulation, et les positions des dégâts le long d'une route. La fonction de densité de probabilité du processus à chaque tranche de temps t est distribuée selon la loi de Poisson.

In[1]:=

PDF[InhomogeneousPoissonProcess[f[\[Tau]], \[Tau]][t], x]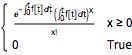

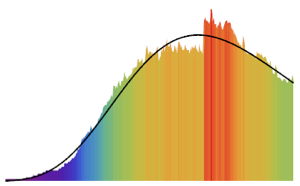
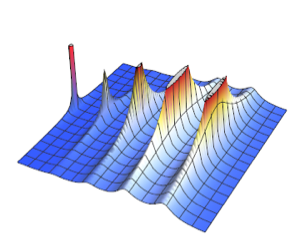
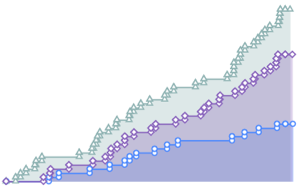
Out[1]=

Simulez un processus de Poisson inhomogène.

In[2]:=

td = RandomFunction[ InhomogeneousPoissonProcess[2 + 1/(1 + t^2), t], {0, 20}];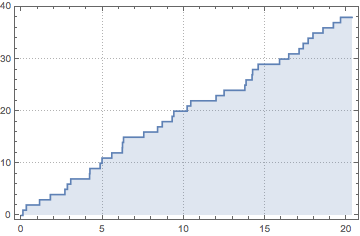

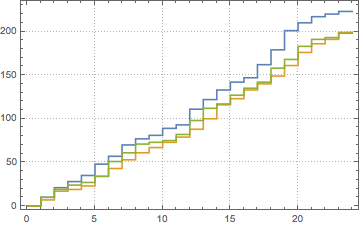
In[3]:=

ListStepPlot[td, Filling -> Axis, ImageSize -> Medium, PlotTheme -> "Detailed"]

Out[3]=

Un processus de Poisson inhomogène peut être utilisé pour modéliser les chiffres d'arrivée. Ici, le processus est utilisé pour simuler le nombre d'arrivées dans un petit fast-food, si les taux horaires d'arrivée des clients sont donnés.

In[4]:=

arrivalrates = {{0, 8}, {1, 9}, {2, 7}, {4, 6}, {5, 12}, {6, 14}, {7, 11}, {8, 6}, {9, 4}, {10, 3}, {11, 8}, {12, 15}, {13, 12}, {14, 10}, {15, 8}, {16, 6}, {17, 12}, {18, 17}, {19, 15}, {20, 12}, {21, 6}, {22, 5}, {23, 7}}; \[Lambda][t_] = Interpolation[arrivalrates, InterpolationOrder -> 1][t];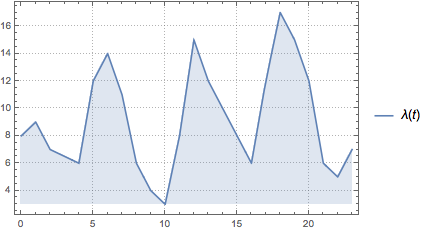

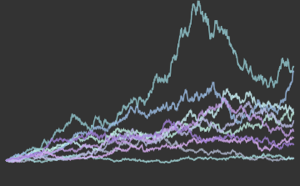
In[5]:=

Plot[\[Lambda][t], {t, 0, 23}, Exclusions -> None, Filling -> Axis, ImageSize -> Medium, PlotTheme -> "Detailed"]

Out[5]=

Définissez un processus de Poisson inhomogène pour les arrivées sur la base de la fonction de taux donnée λ(t) et simulez les nombres d'arrivée dans la journée.

In[6]:=

\[ScriptCapitalP] = InhomogeneousPoissonProcess[\[Lambda][t], t]; td = RandomFunction[\[ScriptCapitalP], {0, 23, 1}, 3];

In[7]:=

ListStepPlot[td, ImageSize -> Medium, PlotTheme -> "Detailed"]

Out[7]=