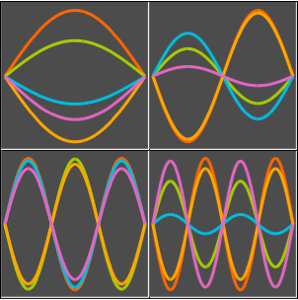
Observez une particule quantique dans une boîte
Une particule quantique libre de se déplacer à l'intérieur d'un rectangle bidimensionnel dont les côtés sont 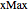 et
et 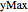 est décrite par l'équation de Schrödinger bidimensionnelle dépendant du temps, ainsi que par des conditions aux limites qui forcent la fonction d'onde à s'annuler à la frontière.
est décrite par l'équation de Schrödinger bidimensionnelle dépendant du temps, ainsi que par des conditions aux limites qui forcent la fonction d'onde à s'annuler à la frontière.
eqn = I D[\[Psi][x, y, t], t] == -\[HBar]^2/(2 m)
Laplacian[\[Psi][x, y, t], {x, y}];bcs = {\[Psi][0, y, t] == 0, \[Psi][xMax, y, t] ==
0, \[Psi][x, yMax, t] == 0, \[Psi][x, 0, t] == 0};Cette équation a une solution générale qui est une somme infinie formelle de ce qu'on appelle les états propres.
DSolveValue[{eqn, bcs}, \[Psi][x, y, t], {x, y, t}]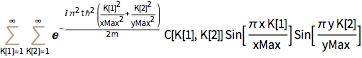
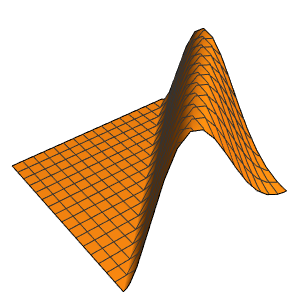
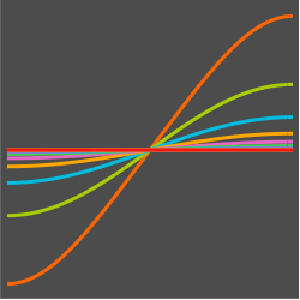
Définissez une condition initiale égale à un état propre.
initEigen = \[Psi][x, y, 0] ==
2 /Sqrt[xMax yMax] Sin[(\[Pi] x)/xMax] Sin[(\[Pi] y)/yMax];Dans ce cas, la solution est simplement un multiple dépendant du temps (de module unitaire) de la condition initiale.
DSolveValue[{eqn, bcs, initEigen}, \[Psi][x, y, t], {x, y, t}]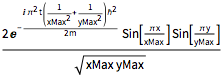
Définissez une condition initiale qui est une somme d'états propres. Comme les conditions initiales ne sont pas un état propre, la densité de probabilité de l'emplacement de la particule dépendra du temps.
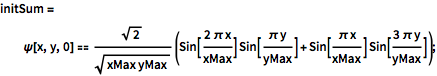
initSum = \[Psi][x, y, 0] ==
Sqrt[2]/Sqrt[
xMax yMax] (Sin[(2 \[Pi] x)/xMax] Sin[(\[Pi] y)/yMax] +
Sin[(\[Pi] x)/xMax] Sin[(3 \[Pi] y)/yMax]);Résolvez-la avec la nouvelle condition initiale.
sol = DSolveValue[{eqn, bcs, initSum}, \[Psi][x, y, t], {x, y, t}]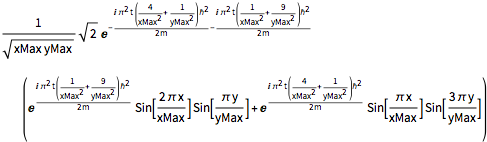
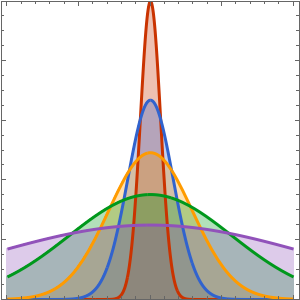
Calculez la densité de probabilité en insérant les valeurs de la constante de Planck réduite, de la masse des électrons et d'une boîte de taille atomique, en utilisant les unités de masse des électrons, les nanomètres et les femtosecondes.
\[HBar] =
QuantityMagnitude[Quantity[1., "ReducedPlanckConstant"],
"ElectronMass" * ("Nanometers")^2/"Femtoseconds"]\[Rho][x_, y_, t_] =
FullSimplify[ComplexExpand[Conjugate[sol] sol]] /. {m -> 1,
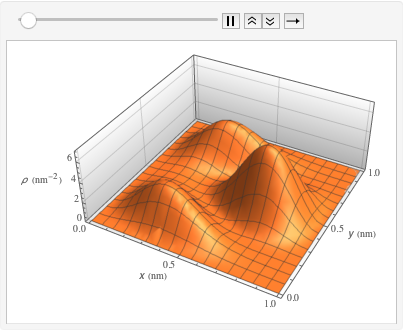
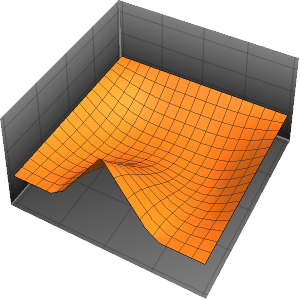
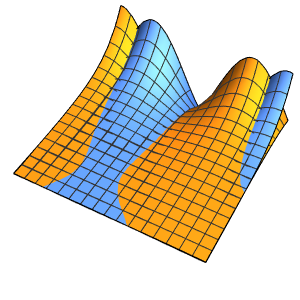
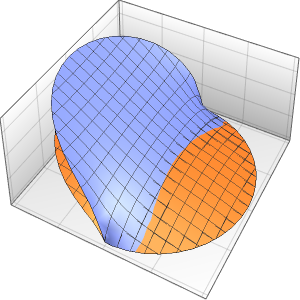
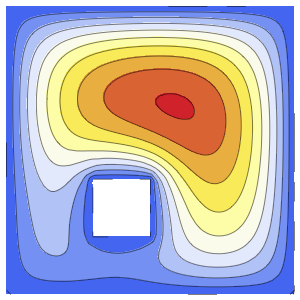
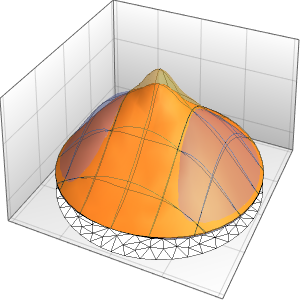
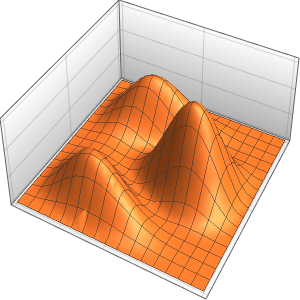
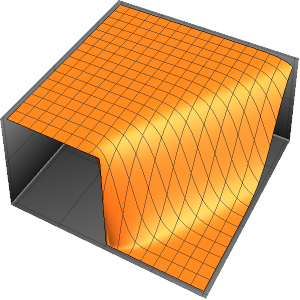
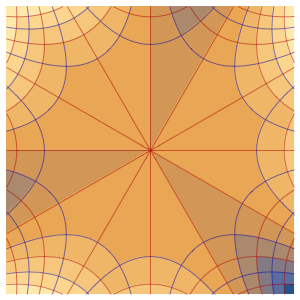
xMax -> 1, yMax -> 1}Visualisez la densité de probabilité à l'intérieur de la boîte dans le temps.

ListAnimate[
Table[Plot3D[\[Rho][x , y , t], {x, 0, 1}, {y, 0, 1},
PlotTheme -> {"Scientific", "SolidGrid"}, AxesLabel -> {"\!\(\*
StyleBox[\"x\", \"SO\"]\) (nm)", " \!\(\*
StyleBox[\"y\", \"SO\"]\) (nm)", "\!\(\*
StyleBox[\"\[Rho]\", \"SO\"]\) (\!\(\*SuperscriptBox[\(nm\), \
\(-2\)]\))"}, ImageSize -> Medium, PlotRange -> {0, 7}], {t, 0,
19, .5}]]