Construisez une fonction analytique complexe
Construisez une fonction analytique complexe à partir des valeurs de ses parties réelles et imaginaires sur l'axe des 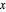 .
.
Les parties réelles et imaginaires u et v satisfont les équations de Cauchy–Riemann.
In[1]:=
creqns = {D[u[x, y], x] == D[v[x, y], y],
D[v[x, y], x] == -D[u[x, y], y]};Établissez les valeurs de u et de v sur l'axe des 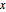 .
.
In[2]:=
xvals = {u[x, 0] == x^3, v[x, 0] == 0};Résolvez les équations de Cauchy–Riemann.
In[3]:=
sol = DSolve[{creqns, xvals}, {u, v}, {x, y}]Out[3]=
Vérifiez que les solutions sont des fonctions harmoniques.
In[4]:=
Laplacian[{u[x, y], v[x, y]} /. sol[[1]], {x, y}]Out[4]=
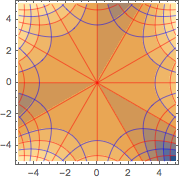
Visualisez les lignes de courant et les équipotentielles générées par la solution.
In[5]:=
ContourPlot[{u[x, y], v[x, y]} /. sol[[1]], {x, -5, 5}, {y, -5, 5},
ContourStyle -> {Red, Blue}]Out[5]=
Construisez une fonction analytique complexe à partir de la solution.
In[6]:=
f[x_, y_] = u[x, y] + I v[x, y] /. sol[[1]]Out[6]=
Cela représente la fonction 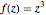 .
.
In[7]:=
(f[x, y] // Factor) /. {x + I y -> z}Out[7]=