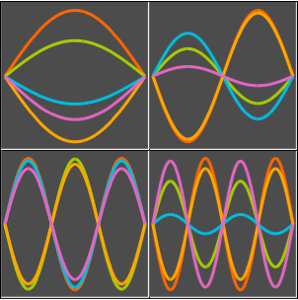
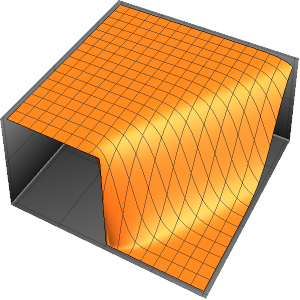
Résolvez une équation d'onde avec des conditions aux limites absorbantes
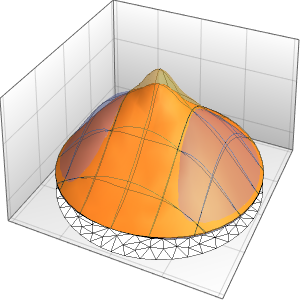
Résolvez une équation d'onde 1D avec des conditions aux limites absorbantes.
Spécifiez une équation d'onde avec l'absorption des conditions aux limites. Veuillez remarquer que la valeur de Neumann est la première dérivée temporelle de 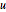 .
.
In[1]:=
eqn = D[u[t, x], {t, 2}] ==
D[u[t, x], {x, 2}] +
NeumannValue[-Derivative[1, 0][u][t, x], x == 0 || x == 1];Spécifiez les conditions initiales pour l'équation d'onde.
In[2]:=
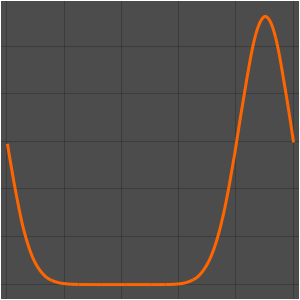
u0[x_] := Evaluate[D[0.125 Erf[(x - 0.5)/0.125], x]];
ic = {u[0, x] == u0[x], Derivative[1, 0][u][0, x] == 0};Résolvez l'équation en utilisant la méthode des éléments finis.
In[3]:=

ufun = NDSolveValue[{eqn, ic}, u, {t, 0, 1}, {x, 0, 1},
Method -> {"MethodOfLines",
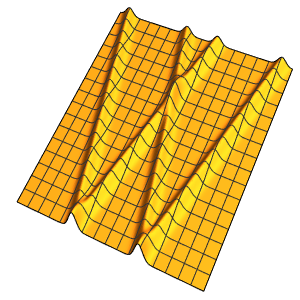
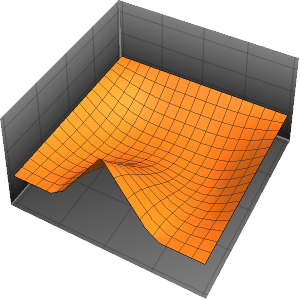
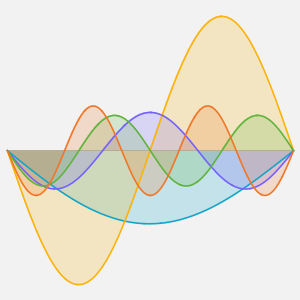
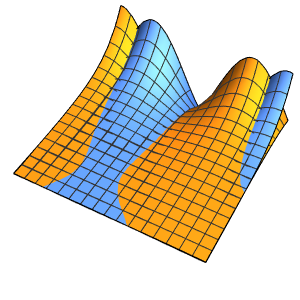
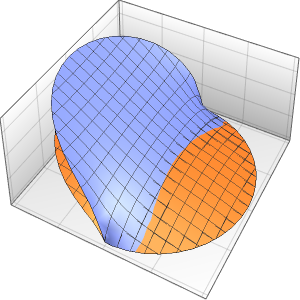
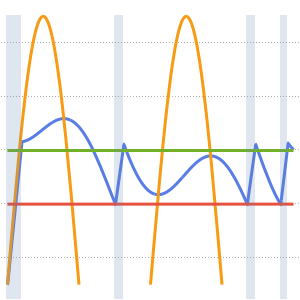
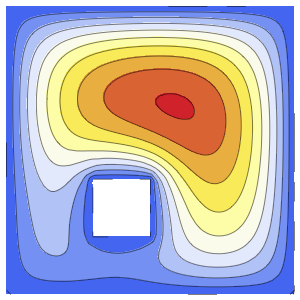
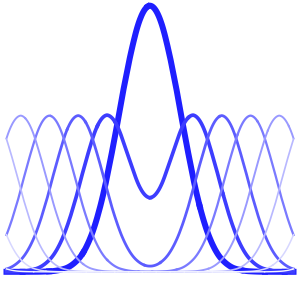
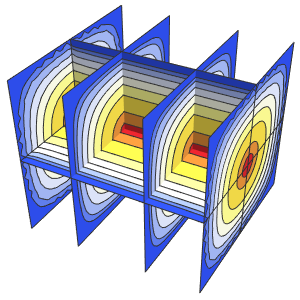
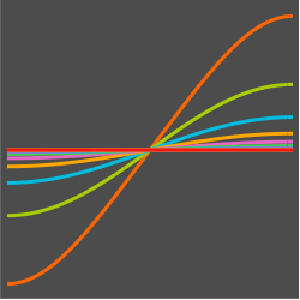
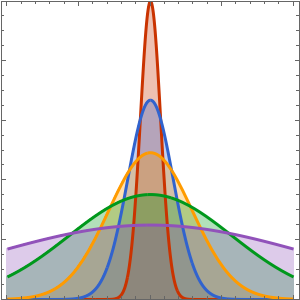
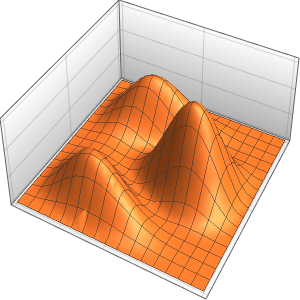
"SpatialDiscretization" -> {"FiniteElement"}}];Visualisez l'équation d'onde avec des conditions aux limites absorbantes.
In[4]:=
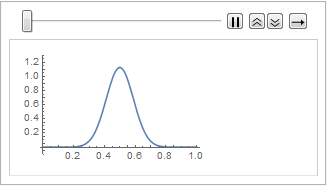
list = Table[
Plot[ufun[t, x], {x, 0, 1}, PlotRange -> {-0.1, 1.3}], {t, 0, 1,
0.1}];
ListAnimate[list]