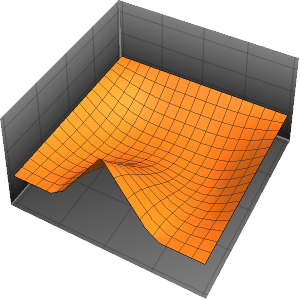
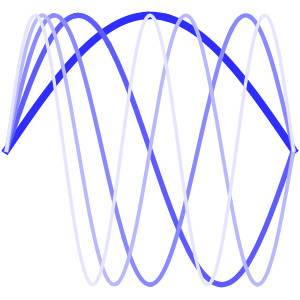
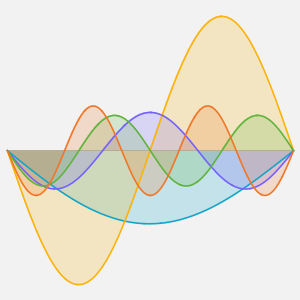
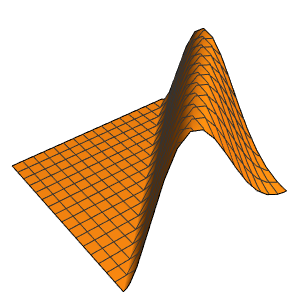
Résolvez l'équation de poisson avec les conditions aux limites périodiques
Résolvez une équation de Poisson avec des conditions aux limites périodiques sur des limites courbes.
Spécifiez une région.
In[1]:=
\[CapitalOmega] =
RegionDifference[RegionUnion[Disk[], Rectangle[{0, -1}, {2, 1}]],
Disk[{2, 0}]];Résolvez l'équation aux dérivées partielles avec des conditions aux limites périodiques où la solution du côté gauche est appliqué à travers le côté droit de la région.
In[2]:=

ufun = NDSolveValue[{-\!\(
\*SubsuperscriptBox[\(\[Del]\), \({x, y}\), \(2\)]\(u[x, y]\)\) == 1,
PeriodicBoundaryCondition[u[x, y], (x - 2)^2 + y^2 == 1,
Function[x, x - {2, 0}]],
DirichletCondition[
u[x, y] == 0, (0 <= x < 2 - 10^-6 2 && (y <= -1 || y >= 1))]},
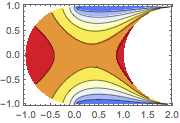
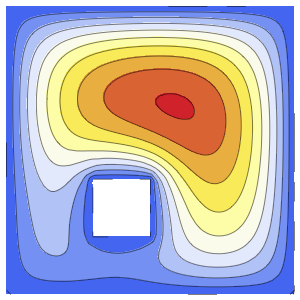
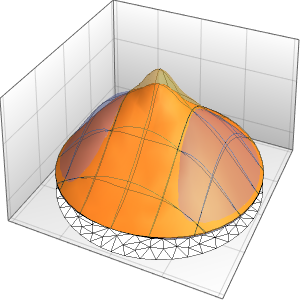
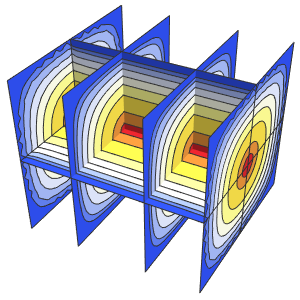
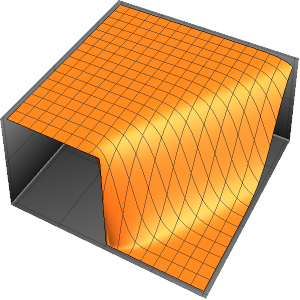
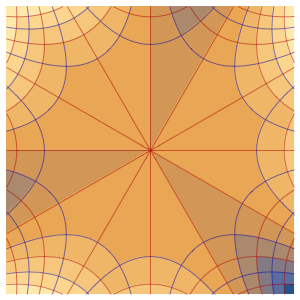
u, {x, y} \[Element] \[CapitalOmega]];Visualisez la solution.
In[3]:=
ContourPlot[ufun[x, y], {x, y} \[Element] \[CapitalOmega],
ColorFunction -> "TemperatureMap", AspectRatio -> Automatic]Out[3]=