Résolvez un problème de valeur initiale pour l'équation de l'onde
Spécifiez l'équation d'onde avec la vitesse de l'unité de propagation.
In[1]:=
weqn = D[u[x, t], {t, 2}] == D[u[x, t], {x, 2}];Définissez les conditions initiales pour l'équation.
In[2]:=
ic = {u[x, 0] == E^(-x^2), Derivative[0, 1][u][x, 0] == 1};Résolvez le problème de la valeur initiale.
In[3]:=
DSolveValue[{weqn, ic}, u[x, t], {x, t}]Out[3]=
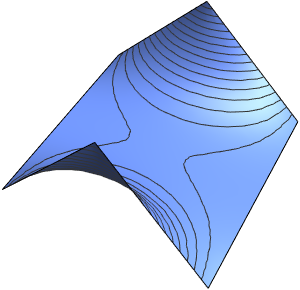
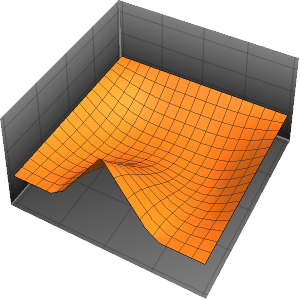
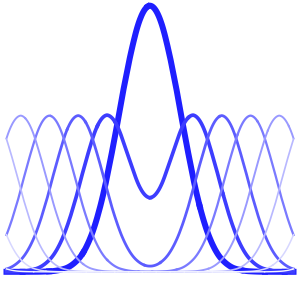
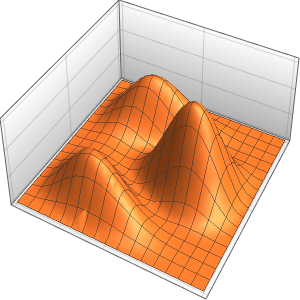
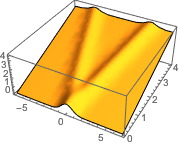
L'onde se propage le long d'une paire de directions caractéristiques.
In[4]:=
DSolveValue[{weqn, ic}, u[x, t], {x, t}];
Plot3D[%, {x, -7, 7}, {t, 0, 4}, Mesh -> None]Out[4]=
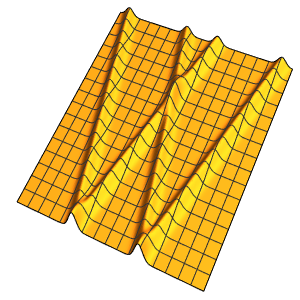
Résolvez le problème de la valeur initiale des données par morceaux.
In[5]:=
ic = {u[x, 0] == UnitBox[x] + UnitTriangle[x/3],
Derivative[0, 1][u][x, 0] == 0};In[6]:=
DSolveValue[ {weqn, ic}, u[x, t], {x, t}]Out[6]=
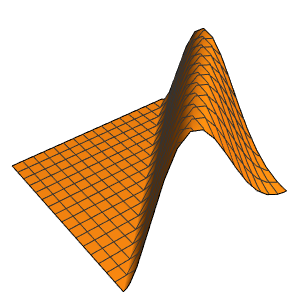
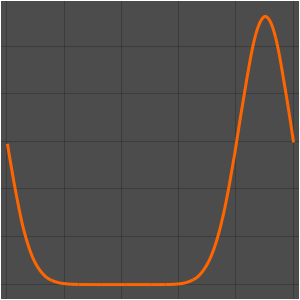
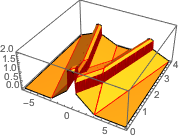
Les discontinuités dans les données initiales sont propagées le long des directions caractéristiques.
In[7]:=
DSolveValue[ {weqn, ic}, u[x, t], {x, t}];
Plot3D[%, {x, -7, 7}, {t, 0, 4}, PlotRange -> All, Mesh -> None,
ExclusionsStyle -> Red]Out[7]=
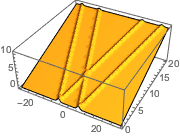
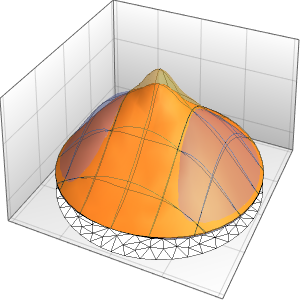
Résolvez le problème de la valeur initiale avec une somme de fonctions exponentielles comme données initiales.
In[8]:=
ic = {u[x, 0] == E^(-(x - 6)^2) + E^(-(x + 6)^2),
Derivative[0, 1][u][x, 0] == 1/2};In[9]:=
sol = DSolveValue[ {weqn, ic}, u[x, t], {x, t}]Out[9]=
Visualisez la solution.
In[10]:=
Plot3D[sol, {x, -30, 30}, {t, 0, 20}, PlotRange -> All, Mesh -> None,
PlotPoints -> 30]Out[10]=