Résolvez un problème de valeur initiale pour un système hyperbolique linéaire
Spécifiez un système hyperbolique linéaire inhomogène à coefficients constants.
In[1]:=
eqns = {D[u[x, t], t] == D[v[x, t], x] + 1,
D[v[x, t], t] == -D[u[x, t], x] - 1};Définissez les conditions initiales pour le système.
In[2]:=
ic = {u[x, 0] == Cos[x]^2, v[x, 0] == Sin[x]};Résolvez le système à l'aide de DSolveValue.
In[3]:=
sol = DSolveValue[{eqns, ic}, {u[x, t], v[x, t]}, {x, t}] //
FullSimplifyOut[3]=
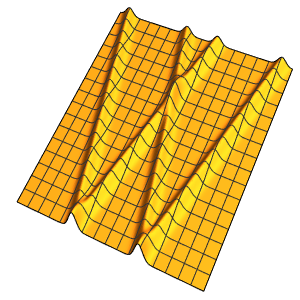
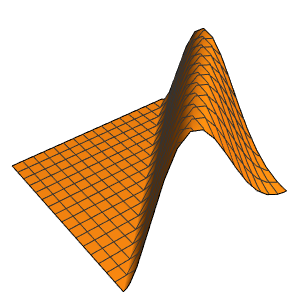
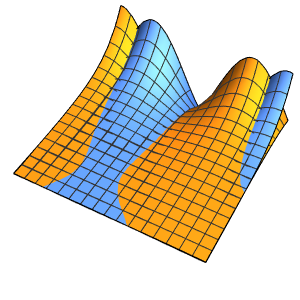
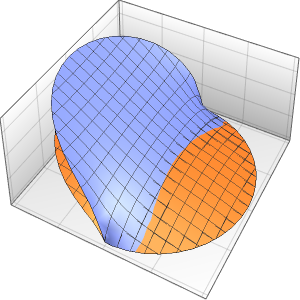
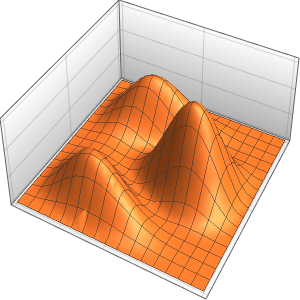
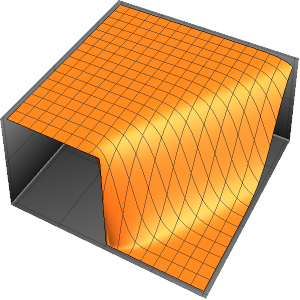
Visualisez la solution.
In[4]:=
Plot3D[sol // Evaluate, {x, 0, 4}, {t, 0, 3}, PlotRange -> {-70, 120}]Out[4]=