Trouvez la valeur d'une option d'achat européenne

Trouvez la valeur d'une option d'achat européenne de vanille si le prix de l'actif sous-jacent et le prix d'exercice sont à la fois 100 $, le taux sans risque est de 6%, la volatilité de l'actif sous-jacent est de 20%, et la période de maturité est d'un an, en utilisant le modèle de Black–Scholes.

In[1]:=

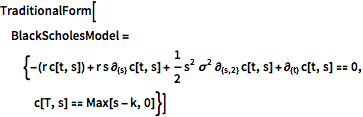
TraditionalForm[BlackScholesModel = {-(r c[t, s]) + r s \!\( \*SubscriptBox[\(\[PartialD]\), \({s}\)]\(c[t, s]\)\) + 1/2 s^2 \[Sigma]^2 \!\( \*SubscriptBox[\(\[PartialD]\), \({s, 2}\)]\(c[t, s]\)\) + \!\( \*SubscriptBox[\(\[PartialD]\), \({t}\)]\(c[t, s]\)\) == 0, c[T, s] == Max[s - k, 0]}]

Out[1]//TraditionalForm=

Résolvez le problème de valeur de limite.

In[2]:=

(dsol = c[t, s] /. DSolve[BlackScholesModel, c[t, s], {t, s}][[ 1]]) // TraditionalForm

Out[2]//TraditionalForm=

Calculez la valeur de l'option de vanille européenne.

In[3]:=

dsol /. {t -> 0, s -> 100, k -> 100, \[Sigma] -> 0.2, T -> 1, r -> 0.06}

Out[3]=

Comparez avec la valeur donnée par la fonction FinancialDerivative.

In[4]:=

FinancialDerivative[{"European", "Call"}, {"StrikePrice" -> 100.00, "Expiration" -> 1}, {"InterestRate" -> 0.06, "Volatility" -> 0.2 , "CurrentPrice" -> 100}]

Out[4]=