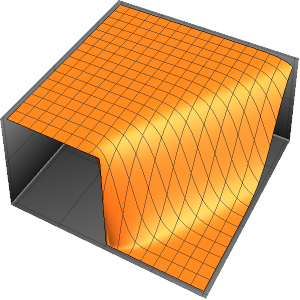
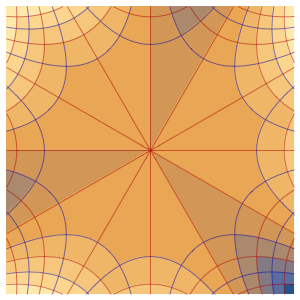
Étudiez la dispersion en mécanique quantique
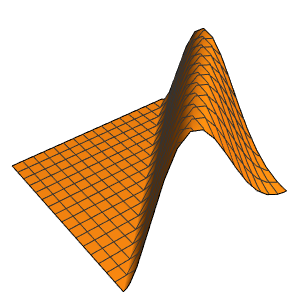
Résolvez l'équation de Schrödinger unidimensionnelle pour une particule libre qui est initialement fortement localisée autour de 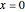 .
.
In[1]:=
eqn = I D[\[Psi][x, t], t] == D[\[Psi][x, t], {x, 2}];
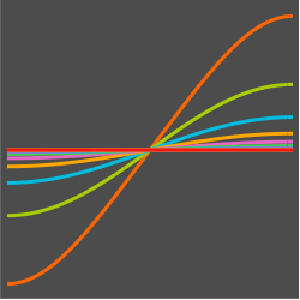
sol[x_, t_] =
DSolveValue[{eqn, \[Psi][x, 0] == Exp[-x^2]}, \[Psi][x, t], {x, t}]Out[1]=
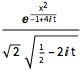
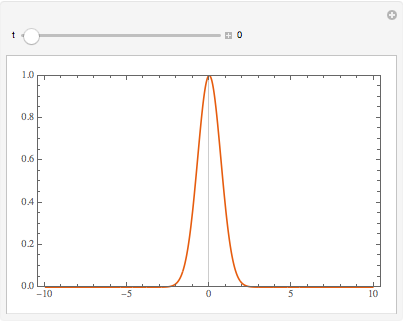
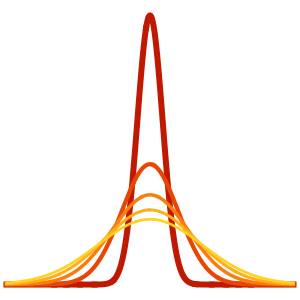
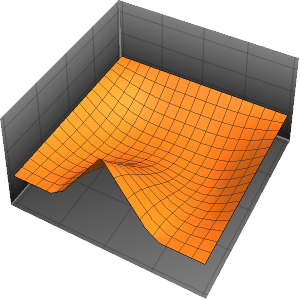
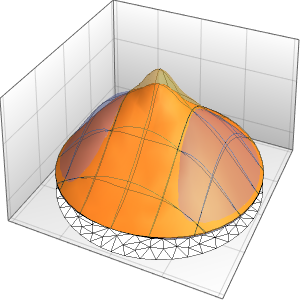
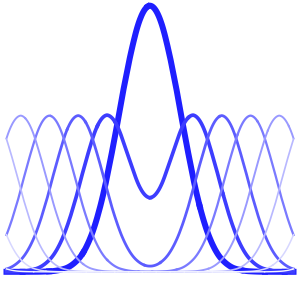
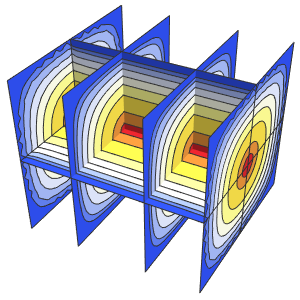
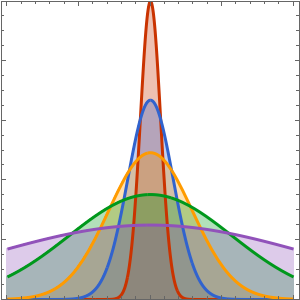
Au fur et à mesure que le temps s'écoule, la fonction d'onde présente un pic moins marqué à l'origine.
In[2]:=

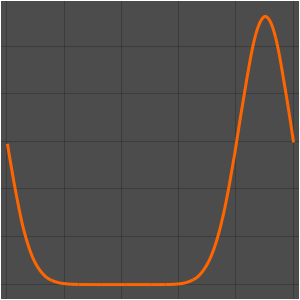
Manipulate[
Plot[Abs@sol[x, t], {x, -10, 10}, PlotRange -> {0, 1},
PlotTheme -> "Scientific", ImageSize -> Medium], {t, 0, 5,
Appearance -> "Labeled"}]