Résolvez un problème de valeur initiale pour l'équation de la chaleur

Spécifiez l'équation de la chaleur.

In[1]:=

heqn = D[u[x, t], t] == D[u[x, t], {x, 2}];

Établissez une condition initiale pour l'équation.

In[2]:=

ic = u[x, 0] == E^(-x^2);

Résolvez le problème de la valeur initiale.

In[3]:=

sol = DSolveValue[{heqn, ic }, u[x, t], {x, t}]

Out[3]=

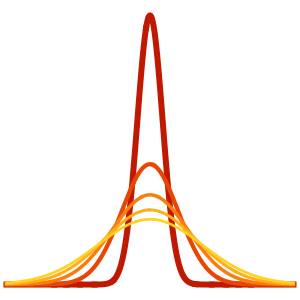
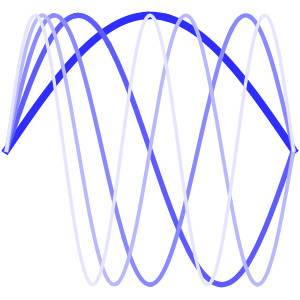
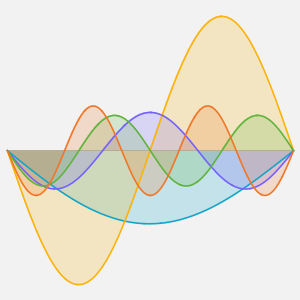
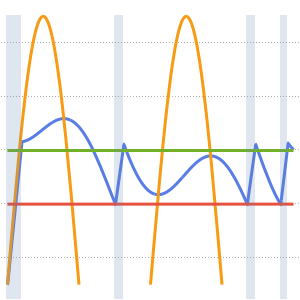
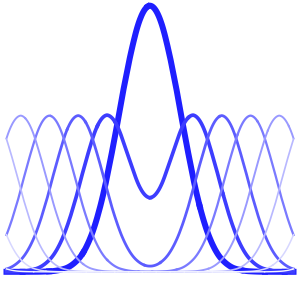
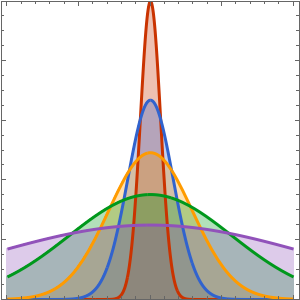
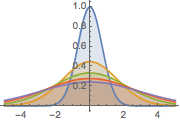
Visualisez la diffusion de la chaleur avec le passage du temps.

In[4]:=

Plot[Evaluate[Table[sol, {t, 0, 4}]], {x, -5, 5}, PlotRange -> All, Filling -> Axis]

Out[4]=

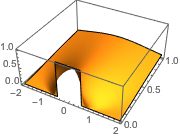
Problème de valeur initiale pour l'équation de la chaleur avec des données initiales par morceaux.

In[5]:=

ic = u[x, 0] == UnitBox[x];

In[6]:=

sol = DSolveValue[{heqn, ic }, u[x, t], {x, t}]

Out[6]=

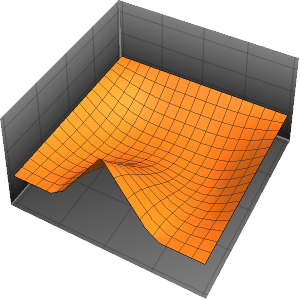
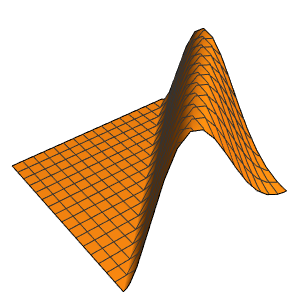
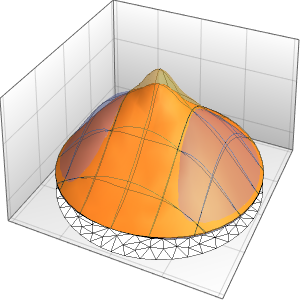
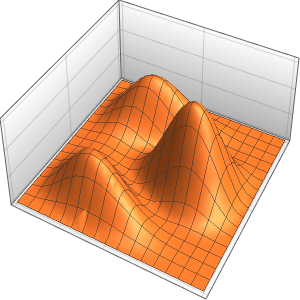
Les discontinuités dans les données initiales sont lissées instantanément.

In[7]:=

Plot3D[sol, {x, -2, 2}, {t, 0, 1}, PlotRange -> All, PlotPoints -> 250, Mesh -> None]

Out[7]=