Distribuição de matriz normal e matriz T

Distribuições de matriz normal e matriz 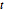são distribuições de matriz normal variante e 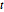com matrizes de escala de linha e coluna específicas. Os usos comuns incluem a análise de séries temporais, processos aleatórios, e regressão multivariada.

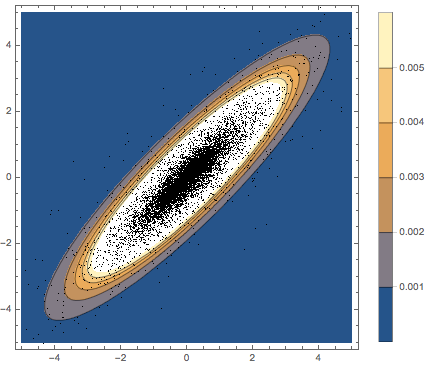
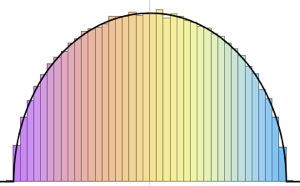
Dadas as matrizes de escala Σ_row e Σ_col, a distribuição normal de matriz tem uma densidade de probabilidade proporcional a 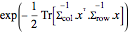. Faça uma amostra de uma distribuição normal de matriz.

In[1]:=

Subscript[\[CapitalSigma], row] = {{1, 0.9}, {0.9, 1}}; Subscript[\[CapitalSigma], col] = {{1, -0.9}, {-0.9, 1}};

In[2]:=

RandomVariate[ MatrixNormalDistribution[Subscript[\[CapitalSigma], row], Subscript[\[CapitalSigma], col]]]

Out[2]=

Visualize os vetores em linha amostrados em um gráfico de dispersão e compare-o com a função de densidade.

In[3]:=

sample = RandomVariate[ MatrixNormalDistribution[Subscript[\[CapitalSigma], row], Subscript[\[CapitalSigma], col]], 10^4]; firstrows = sample[[All, 1]];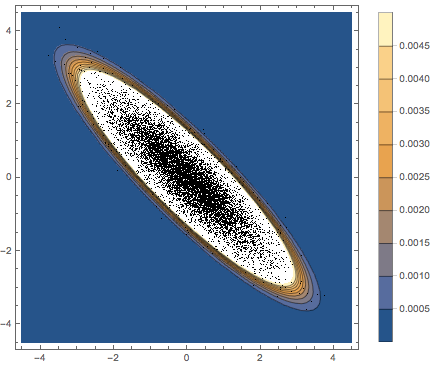

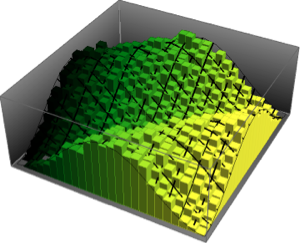
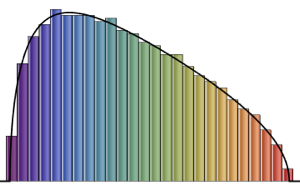
In[4]:=

Show[ContourPlot[ PDF[MultinormalDistribution[{0, 0}, Subscript[\[CapitalSigma], col] ], {x, y}], {x, -4.5, 4.5}, {y, -4.5, 4.5}, PlotPoints -> 30, PlotTheme -> "Detailed", ImageSize -> Medium], ListPlot[firstrows, ImageSize -> Medium, PlotTheme -> "Detailed", PlotStyle -> Black]]

Out[4]=

Visualize os vetores da coluna amostrados em um histograma e compare-o com a função de densidade.

In[5]:=

firstcols = sample[[All, All, 1]];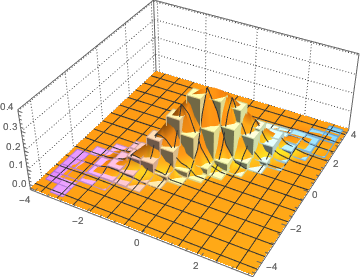

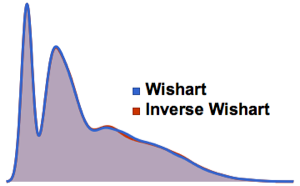
In[6]:=

Show[Histogram3D[firstcols, Automatic, "PDF", ImageSize -> Medium, PlotTheme -> "Detailed", ChartStyle -> "Pastel"], Plot3D[PDF[ MultinormalDistribution[{0, 0}, Subscript[\[CapitalSigma], row] ], {x, y}], {x, -5, 5}, {y, -5, 5}, PlotRange -> All, ImageSize -> Medium, PlotTheme -> "Detailed", PlotLegends -> None]]

Out[6]=

Similar às distribuições 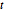de Student e multivariada, a distribuição 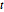de matriz é uma mescla de distribuição normal de matriz com parâmetro de escala de distribuição de Wishart inversa. Faça uma amostra de uma distribuição 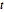de matriz.

In[7]:=

RandomVariate[ MatrixTDistribution[Subscript[\[CapitalSigma], row], Subscript[\[CapitalSigma], col], 3]]

Out[7]=

Gere um conjunto de matrizes distribuídas de matriz .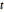

In[8]:=

sample = RandomVariate[ MatrixTDistribution[Subscript[\[CapitalSigma], row], Subscript[\[CapitalSigma], col], 3], 10^4];

As projeções de menor dimensão de variáveis distribuídas com matriz 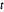são distribuições 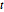de Student e de 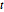multivariada. Projete a amostra em vetores bidimensionais e verifique a qualidade do ajuste.

In[9]:=

v = {1, 2}; vecs = sample.v;

In[10]:=

DistributionFitTest[vecs, MultivariateTDistribution[ Subscript[\[CapitalSigma], row] (v.Subscript[\[CapitalSigma], col].v)/3, 3]]

Out[10]=

Visualize os dados projetados em um gráfico de dispersão e compare-o com a função de densidade.

In[11]:=

Show[ContourPlot[ PDF[MultivariateTDistribution[ Subscript[\[CapitalSigma], row] (v.Subscript[\[CapitalSigma], col].v)/3, 3], {x, y}], {x, -5, 5}, {y, -5, 5}, PlotPoints -> 30, PlotTheme -> "Detailed", ImageSize -> Medium], ListPlot[vecs, ImageSize -> Medium, PlotTheme -> "Detailed", PlotStyle -> Black]]

Out[11]=