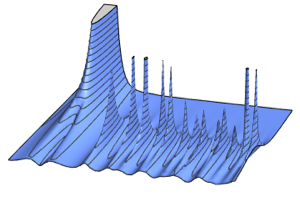
행렬 정규 분포와 행렬 T 분포

행렬 정규 분포와 행렬 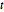분포는 지정된 행과 열 스케일 행렬을 가지는, 행렬이 변수인 정규 분포와 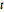분포이며, 주요 적용 분야는 시계열 분석, 확률 과정 다변량 회귀 등이 있습니다.

주어진 스케일 행렬을 Σ_row와 Σ_col 할때, 행렬 정규 분포의 확률 밀도는 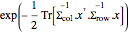에 비례합니다. 정규 분포에서 샘플을 추출합니다.

In[1]:=

Subscript[\[CapitalSigma], row] = {{1, 0.9}, {0.9, 1}}; Subscript[\[CapitalSigma], col] = {{1, -0.9}, {-0.9, 1}};

In[2]:=

RandomVariate[ MatrixNormalDistribution[Subscript[\[CapitalSigma], row], Subscript[\[CapitalSigma], col]]]

Out[2]=

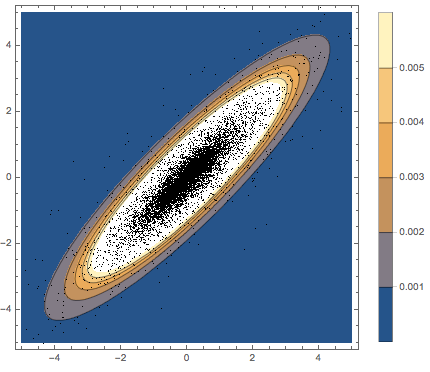
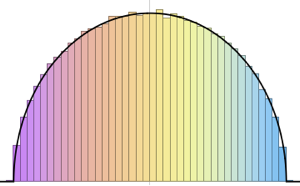
추출된 행 벡터를 분산형으로 시각화하고 밀도 함수와 비교합니다.

In[3]:=

sample = RandomVariate[ MatrixNormalDistribution[Subscript[\[CapitalSigma], row], Subscript[\[CapitalSigma], col]], 10^4]; firstrows = sample[[All, 1]];

In[4]:=

Show[ContourPlot[ PDF[MultinormalDistribution[{0, 0}, Subscript[\[CapitalSigma], col] ], {x, y}], {x, -4.5, 4.5}, {y, -4.5, 4.5}, PlotPoints -> 30, PlotTheme -> "Detailed", ImageSize -> Medium], ListPlot[firstrows, ImageSize -> Medium, PlotTheme -> "Detailed", PlotStyle -> Black]]

Out[4]=

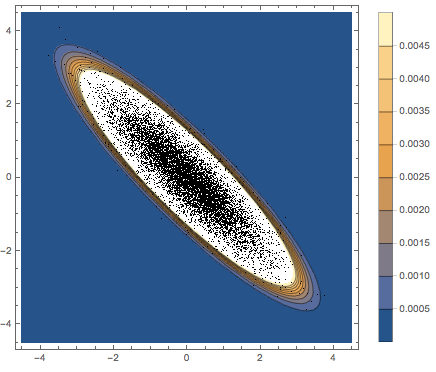
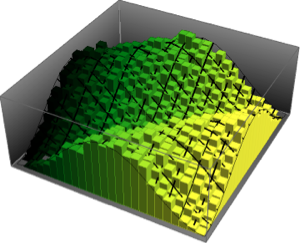
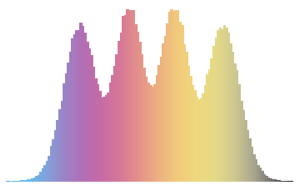
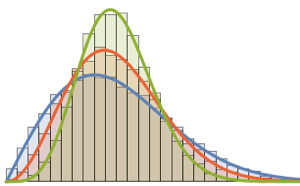
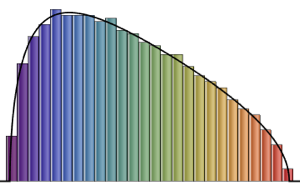
추출된 열 벡터를 히스토그램으로 시각화하고 밀도 함수와 비교합니다.

In[5]:=

firstcols = sample[[All, All, 1]];

In[6]:=

Show[Histogram3D[firstcols, Automatic, "PDF", ImageSize -> Medium, PlotTheme -> "Detailed", ChartStyle -> "Pastel"], Plot3D[PDF[ MultinormalDistribution[{0, 0}, Subscript[\[CapitalSigma], row] ], {x, y}], {x, -5, 5}, {y, -5, 5}, PlotRange -> All, ImageSize -> Medium, PlotTheme -> "Detailed", PlotLegends -> None]]

Out[6]=

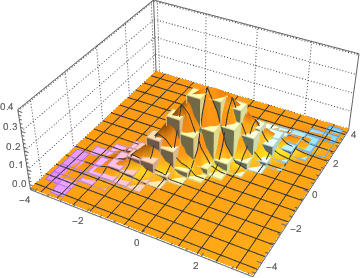
스튜던트 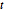분포와 다변량 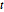분포와 마찬가지로 행렬 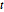분포는 행렬 정규 분포에 역 위샤트 분포의 척도 모수를 섞은 것입니다. 행렬 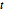분포에서 샘플을 추출합니다.

In[7]:=

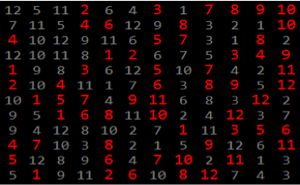
RandomVariate[ MatrixTDistribution[Subscript[\[CapitalSigma], row], Subscript[\[CapitalSigma], col], 3]]

Out[7]=

행렬 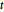분포 행렬의 집합을 생성합니다.

In[8]:=

sample = RandomVariate[ MatrixTDistribution[Subscript[\[CapitalSigma], row], Subscript[\[CapitalSigma], col], 3], 10^4];

행렬 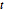분포 변량의 저차원 프로젝션은 스튜던트 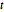분포 및 다변량 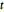분포입니다. 2차원 벡터의 샘플을 프로젝트하고, 추구 적합도를 확인합니다.

In[9]:=

v = {1, 2}; vecs = sample.v;

In[10]:=

DistributionFitTest[vecs, MultivariateTDistribution[ Subscript[\[CapitalSigma], row] (v.Subscript[\[CapitalSigma], col].v)/3, 3]]

Out[10]=

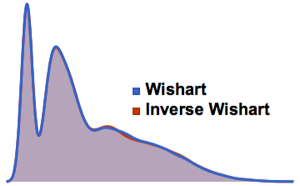
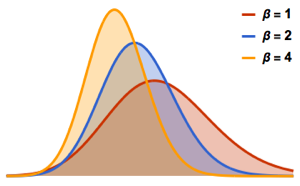
프로젝트된 데이터를 분산형으로 시각화하고 밀도 함수와 비교합니다.

In[11]:=

Show[ContourPlot[ PDF[MultivariateTDistribution[ Subscript[\[CapitalSigma], row] (v.Subscript[\[CapitalSigma], col].v)/3, 3], {x, y}], {x, -5, 5}, {y, -5, 5}, PlotPoints -> 30, PlotTheme -> "Detailed", ImageSize -> Medium], ListPlot[vecs, ImageSize -> Medium, PlotTheme -> "Detailed", PlotStyle -> Black]]

Out[11]=