Distribuciones de matriz normal y matriz T

Las distribuciones de matriz normal y de matriz 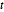son distribuciones de matriz normal variante aleatoria y 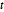con matrices de escala de fila y columna específicas. Los usos típicos incluyen el análisis de series temporales, procesos aleatorios y regresión multivariante.

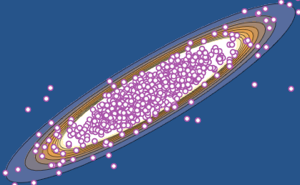
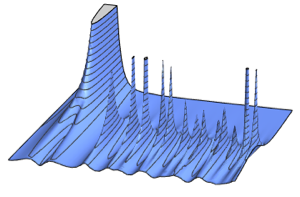
Dadas las matrices de escala Σ_row y Σ_col, la distribución normal de matriz tiene una densidad de probabilidad proporcional a 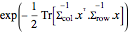. Muestra de una distribución normal de matriz.

In[1]:=

Subscript[\[CapitalSigma], row] = {{1, 0.9}, {0.9, 1}}; Subscript[\[CapitalSigma], col] = {{1, -0.9}, {-0.9, 1}};

In[2]:=

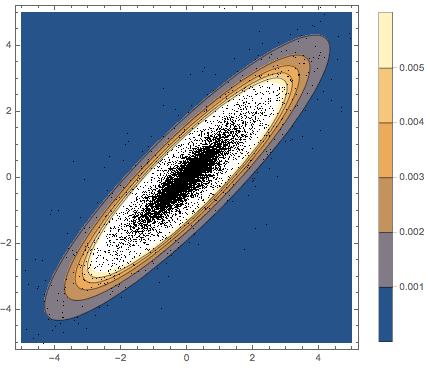
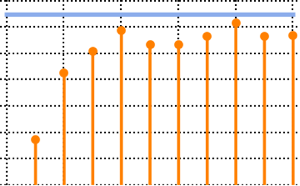
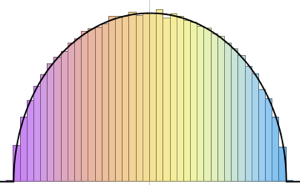
RandomVariate[ MatrixNormalDistribution[Subscript[\[CapitalSigma], row], Subscript[\[CapitalSigma], col]]]

Out[2]=

Visualice los vectores en fila muestreados en un gráfico de dispersión y compárelo con la función de densidad.

In[3]:=

sample = RandomVariate[ MatrixNormalDistribution[Subscript[\[CapitalSigma], row], Subscript[\[CapitalSigma], col]], 10^4]; firstrows = sample[[All, 1]];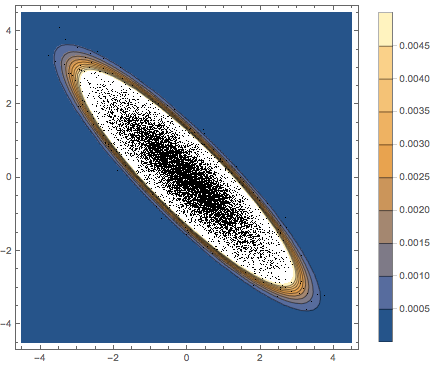

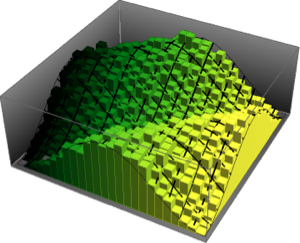
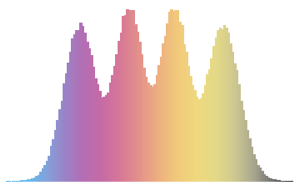
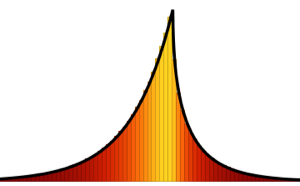
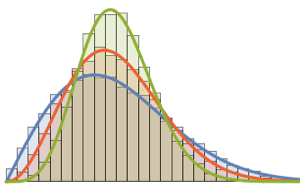
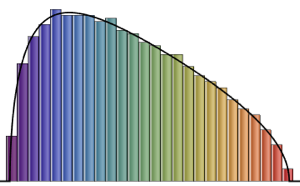
In[4]:=

Show[ContourPlot[ PDF[MultinormalDistribution[{0, 0}, Subscript[\[CapitalSigma], col] ], {x, y}], {x, -4.5, 4.5}, {y, -4.5, 4.5}, PlotPoints -> 30, PlotTheme -> "Detailed", ImageSize -> Medium], ListPlot[firstrows, ImageSize -> Medium, PlotTheme -> "Detailed", PlotStyle -> Black]]

Out[4]=

Visualice los vectores de columna muestreados en un histograma y compárelo con la función de densidad.

In[5]:=

firstcols = sample[[All, All, 1]];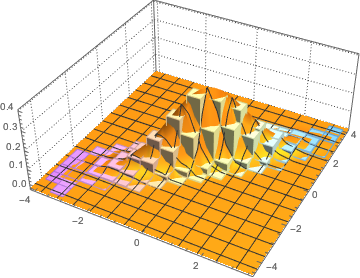

In[6]:=

Show[Histogram3D[firstcols, Automatic, "PDF", ImageSize -> Medium, PlotTheme -> "Detailed", ChartStyle -> "Pastel"], Plot3D[PDF[ MultinormalDistribution[{0, 0}, Subscript[\[CapitalSigma], row] ], {x, y}], {x, -5, 5}, {y, -5, 5}, PlotRange -> All, ImageSize -> Medium, PlotTheme -> "Detailed", PlotLegends -> None]]

Out[6]=

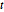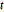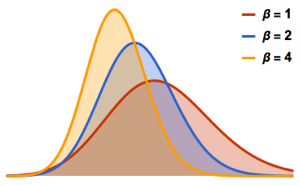
Similar a las distribuciones de Student y multivariante, la distribución 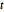de matriz es una mezcla de distribución normal de matriz con parámetro de escala de distribución de Wishart inversa. Muestra de una distribución 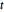de matriz.

In[7]:=

RandomVariate[ MatrixTDistribution[Subscript[\[CapitalSigma], row], Subscript[\[CapitalSigma], col], 3]]

Out[7]=

Genere un conjunto de matrices distribuidas de matriz .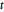

In[8]:=

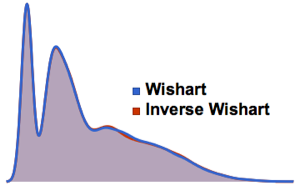
sample = RandomVariate[ MatrixTDistribution[Subscript[\[CapitalSigma], row], Subscript[\[CapitalSigma], col], 3], 10^4];

Las proyecciones de menor dimensión de variables distribuidas con matriz 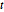son distribuciones de 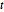de Student y de 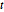multivariante. Proyecte la muestra en vectores bidimensionales y verifique la calidad del ajuste.

In[9]:=

v = {1, 2}; vecs = sample.v;

In[10]:=

DistributionFitTest[vecs, MultivariateTDistribution[ Subscript[\[CapitalSigma], row] (v.Subscript[\[CapitalSigma], col].v)/3, 3]]

Out[10]=

Visualice los datos proyectados en un gráfico de dispersión y compárelo con la función de densidad.

In[11]:=

Show[ContourPlot[ PDF[MultivariateTDistribution[ Subscript[\[CapitalSigma], row] (v.Subscript[\[CapitalSigma], col].v)/3, 3], {x, y}], {x, -5, 5}, {y, -5, 5}, PlotPoints -> 30, PlotTheme -> "Detailed", ImageSize -> Medium], ListPlot[vecs, ImageSize -> Medium, PlotTheme -> "Detailed", PlotStyle -> Black]]

Out[11]=