Язык Wolfram Language™

Нормальное и T-распределение матриц

Матричное нормальное и 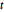-распределения являются варьируемой величиной матричного нормального и 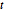-распределения с заданными рядом и столбцом на матричной шкале. Типичное использование включает в себя анализ временных рядов, случайные процессы и многомерную регрессию.

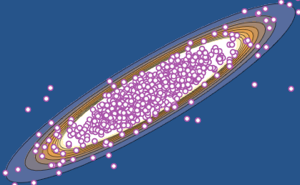
При заданной матричной шкале Σ_row и Σ_col, матрица нормального распределения имеет плотность вероятности пропорциональную 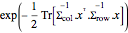. Рассмотрим выборку из матрицы нормального распределения.

In[1]:=

Subscript[\[CapitalSigma], row] = {{1, 0.9}, {0.9, 1}}; Subscript[\[CapitalSigma], col] = {{1, -0.9}, {-0.9, 1}};

In[2]:=

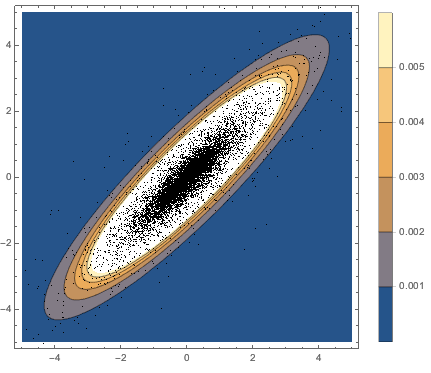
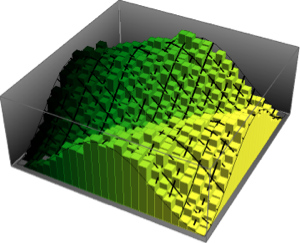
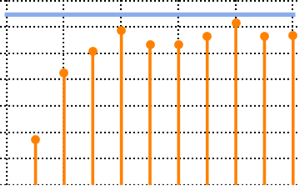
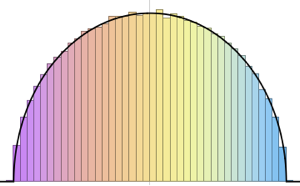
RandomVariate[ MatrixNormalDistribution[Subscript[\[CapitalSigma], row], Subscript[\[CapitalSigma], col]]]

Out[2]=

Визуализируем выборочные векторы строк на графике рассеяния и сравним их с функцией плотности.

In[3]:=

sample = RandomVariate[ MatrixNormalDistribution[Subscript[\[CapitalSigma], row], Subscript[\[CapitalSigma], col]], 10^4]; firstrows = sample[[All, 1]];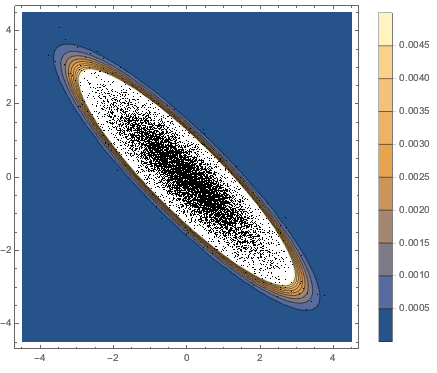

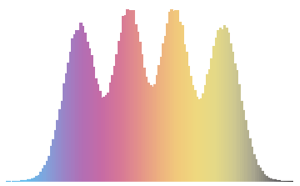
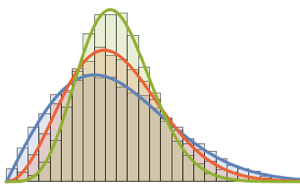
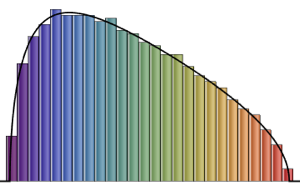
In[4]:=

Show[ContourPlot[ PDF[MultinormalDistribution[{0, 0}, Subscript[\[CapitalSigma], col] ], {x, y}], {x, -4.5, 4.5}, {y, -4.5, 4.5}, PlotPoints -> 30, PlotTheme -> "Detailed", ImageSize -> Medium], ListPlot[firstrows, ImageSize -> Medium, PlotTheme -> "Detailed", PlotStyle -> Black]]

Out[4]=

Визуализируем выборочные векторы столбцов на гистограмме и сравним их с функцией плотности.

In[5]:=

firstcols = sample[[All, All, 1]];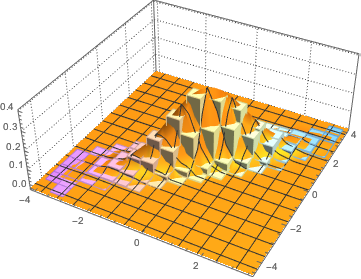

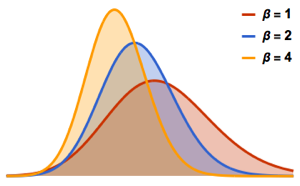
In[6]:=

Show[Histogram3D[firstcols, Automatic, "PDF", ImageSize -> Medium, PlotTheme -> "Detailed", ChartStyle -> "Pastel"], Plot3D[PDF[ MultinormalDistribution[{0, 0}, Subscript[\[CapitalSigma], row] ], {x, y}], {x, -5, 5}, {y, -5, 5}, PlotRange -> All, ImageSize -> Medium, PlotTheme -> "Detailed", PlotLegends -> None]]

Out[6]=

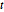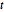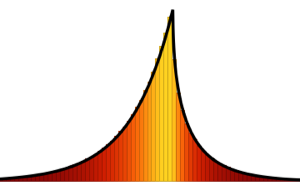
Наряду с -распределением Стьюдента и многомерным -распределением, матричное 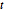-распределение - это сочетание матричного нормального распределения с коэффициентом масштабирования обратного распределения Уишарта. Рассмотрим выборку из матричного 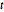-распределения.

In[7]:=

RandomVariate[ MatrixTDistribution[Subscript[\[CapitalSigma], row], Subscript[\[CapitalSigma], col], 3]]

Out[7]=

Сгенерируем набор матриц матричного 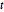-распределения.

In[8]:=

sample = RandomVariate[ MatrixTDistribution[Subscript[\[CapitalSigma], row], Subscript[\[CapitalSigma], col], 3], 10^4];

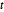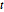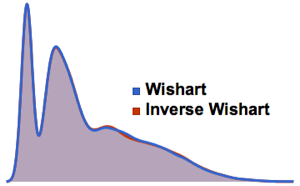
Проекции меньшей размерности переменных матричного -распределения - это варианты -распределения Стьюдента и многомерного 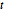-распределения. Спроектируем выборку в двухмерных векторах и проверим критерии согласия.

In[9]:=

v = {1, 2}; vecs = sample.v;

In[10]:=

DistributionFitTest[vecs, MultivariateTDistribution[ Subscript[\[CapitalSigma], row] (v.Subscript[\[CapitalSigma], col].v)/3, 3]]

Out[10]=

Визуализируем спроектированные данные на графике рассеяния и сравним с функцией плотности.

In[11]:=

Show[ContourPlot[ PDF[MultivariateTDistribution[ Subscript[\[CapitalSigma], row] (v.Subscript[\[CapitalSigma], col].v)/3, 3], {x, y}], {x, -5, 5}, {y, -5, 5}, PlotPoints -> 30, PlotTheme -> "Detailed", ImageSize -> Medium], ListPlot[vecs, ImageSize -> Medium, PlotTheme -> "Detailed", PlotStyle -> Black]]

Out[11]=