Lois matricielles normales et lois matricielles T
Les lois matricielles normales et les lois matricielles 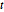 sont des distributions normales de la variante de la matrice et des distributions matricielles
sont des distributions normales de la variante de la matrice et des distributions matricielles 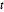 avec des matrices d'échelle de rangée et de colonne spécifiées. L'analyse des séries temporelles, les processus aléatoires et la régression multivariée font partie des utilisations typiques.
avec des matrices d'échelle de rangée et de colonne spécifiées. L'analyse des séries temporelles, les processus aléatoires et la régression multivariée font partie des utilisations typiques.
Étant donné les matrices d'échelle Σrow et Σcol, la loi matricielle normale a une densité de probabilité proportionnelle à 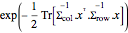 . Échantillonn d'une loi matricielle normale.
. Échantillonn d'une loi matricielle normale.
Subscript[\[CapitalSigma], row] = {{1, 0.9}, {0.9, 1}};
Subscript[\[CapitalSigma], col] = {{1, -0.9}, {-0.9, 1}};RandomVariate[
MatrixNormalDistribution[Subscript[\[CapitalSigma], row],
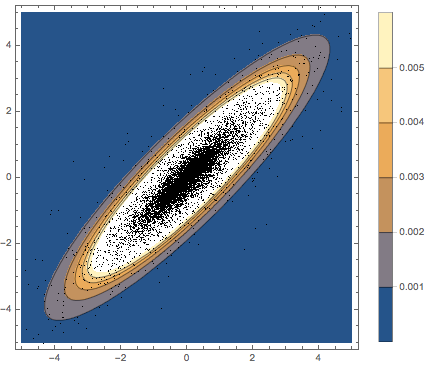
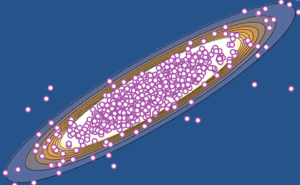
Subscript[\[CapitalSigma], col]]]Visualisez les vecteurs de rangées échantillonnés sur un diagramme de dispersion et comparez-les à la fonction de densité.
sample = RandomVariate[
MatrixNormalDistribution[Subscript[\[CapitalSigma], row],
Subscript[\[CapitalSigma], col]], 10^4];
firstrows = sample[[All, 1]];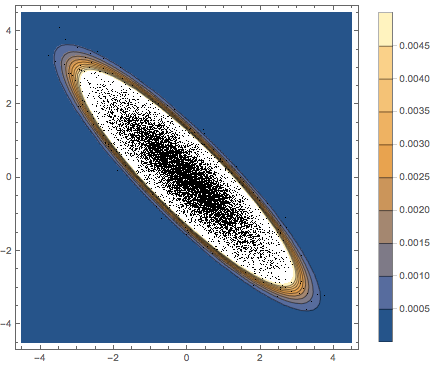
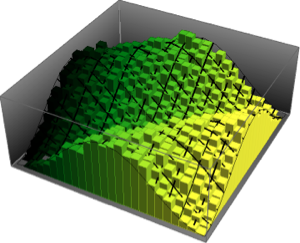
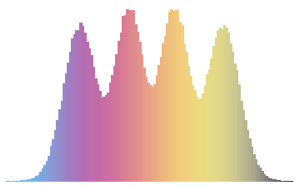
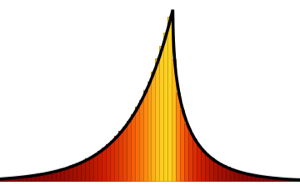
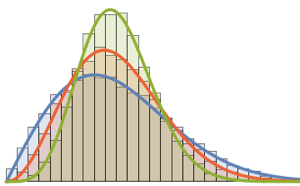
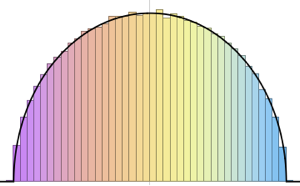
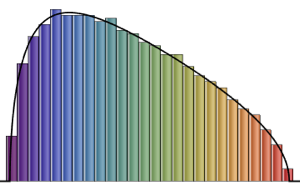
Visualisez les vecteurs de colonnes échantillonnées sur un histogramme et comparez-les avec la fonction de densité.
firstcols = sample[[All, All, 1]];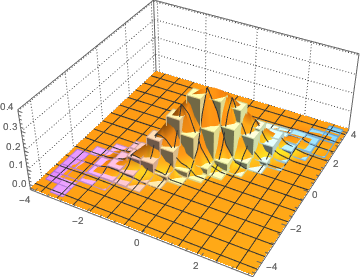
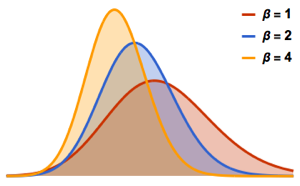
Semblable aux lois 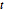 de Student et
de Student et 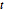 multivariée, la loi matricielle
multivariée, la loi matricielle 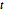 est un mélange de loi normale matricielle avec un paramètre d'échelle distribué à l'inverse de la loi de Wishart. Échantillon d'une loi matricielle
est un mélange de loi normale matricielle avec un paramètre d'échelle distribué à l'inverse de la loi de Wishart. Échantillon d'une loi matricielle 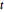 .
.
RandomVariate[
MatrixTDistribution[Subscript[\[CapitalSigma], row],
Subscript[\[CapitalSigma], col], 3]]Générez un ensemble de matrices distribuées 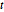 .
.
sample = RandomVariate[
MatrixTDistribution[Subscript[\[CapitalSigma], row],
Subscript[\[CapitalSigma], col], 3], 10^4];Les projections en dimension inférieure des variables distribuées de la matrice 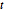 sont distribuées de Student
sont distribuées de Student 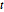 et multivariées
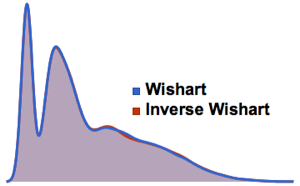
et multivariées 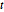 . Projetez l'échantillon sur des vecteurs bidimensionnels et vérifiez la qualité de l'ajustement.
. Projetez l'échantillon sur des vecteurs bidimensionnels et vérifiez la qualité de l'ajustement.
v = {1, 2};
vecs = sample.v;DistributionFitTest[vecs,
MultivariateTDistribution[
Subscript[\[CapitalSigma],
row] (v.Subscript[\[CapitalSigma], col].v)/3, 3]]Visualisez les données projetées sur un diagramme de dispersion et comparez-les avec la fonction de densité.