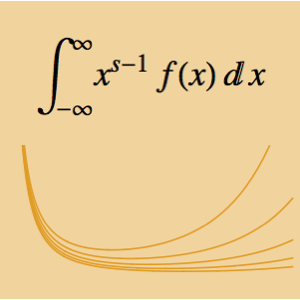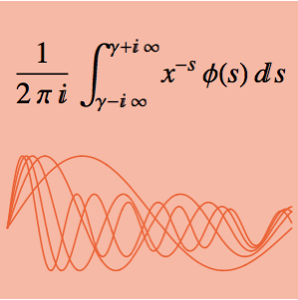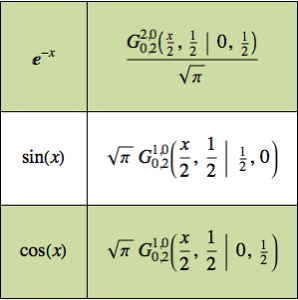G還元を使った定積分を計算する
MeijerGで関数を表すことで，正の実数上での積の計算が可能になる．
関数の積の積分をMeijerG関数で表す規則を生成する．
In[1]:=
IntegrateMeijerG[f_ g_, {z_, 0, Infinity}] /; FreeQ[{f, g}, MeijerG] :=
IntegrateMeijerG[
MeijerGReduce[f, z] MeijerGReduce[g, z], {z, 0, Infinity}]この積分は，厳密に1つのMeijerG式で表すことができる．
In[2]:=
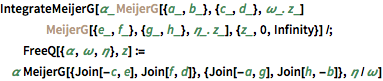
IntegrateMeijerG[\[Alpha]_ Inactive[MeijerG][{a_, b_}, {c_,
d_}, \[Omega]_. z_] Inactive[MeijerG][{e_, f_}, {g_,
h_}, \[Eta]_. z_], {z_, 0, Infinity}] /;
FreeQ[{\[Alpha], \[Omega], \[Eta]},
z] := \[Alpha] MeijerG[{Join[-c, e], Join[f, d]}, {Join[-a, g],
Join[h, -b]}, \[Eta]/\[Omega]]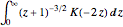
を評価するスキームを適用する．
In[3]:=
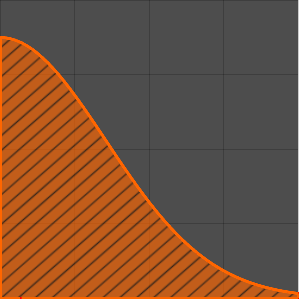
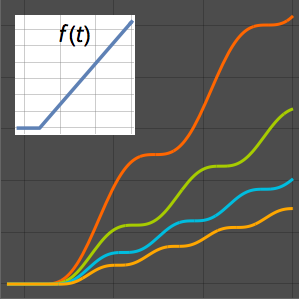
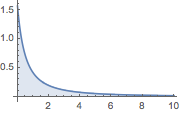
Plot[(1 + z)^(-3/2) EllipticK[-2 z], {z, 0, 10}, Filling -> Axis,
PlotRange -> All]Out[3]=
In[4]:=
IntegrateMeijerG[(1 + z)^(-3/2) EllipticK[-2 z], {z, 0, Infinity}]Out[4]=
Integrateを使って同じ結果を得る．
In[5]:=
Integrate[(1 + z)^(-3/2) EllipticK[-2 z], {z, 0, Infinity}]Out[5]=
答は全く異なるように見えるが，等価である．
In[6]:=
IntegrateMeijerG[(1 + z)^(-3/2) EllipticK[-2 z], {z, 0, Infinity}];
Integrate[(1 + z)^(-3/2) EllipticK[-2 z], {z, 0, Infinity}];
FullSimplify[% == %%]Out[6]=
