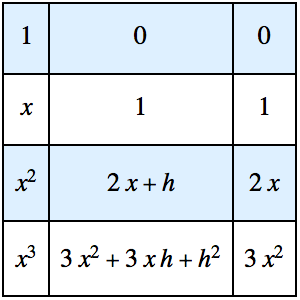
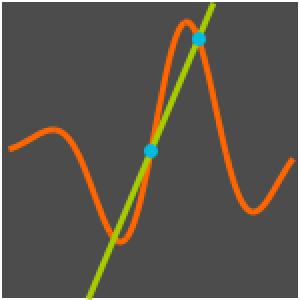
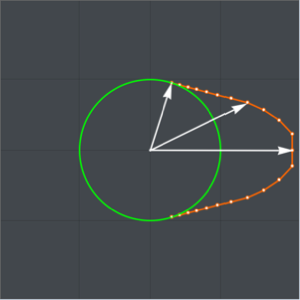
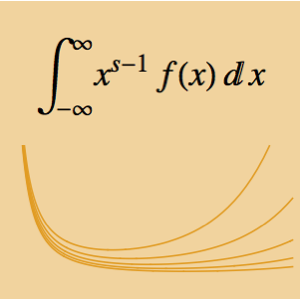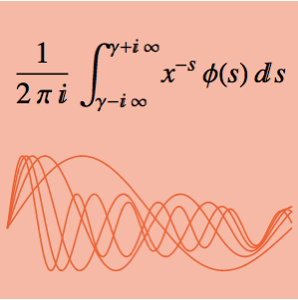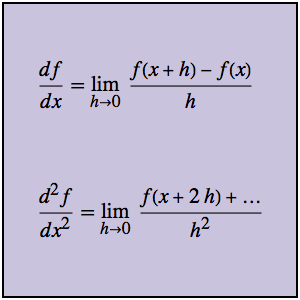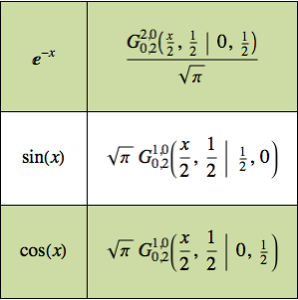G 환원을 이용한 정적분 계산
MeijerG로 함수를 나타내는 것으로, 양의 실수에서 곱의 계산이 가능하게 됩니다.
함수 곱의 적분을 MeijerG 함수로 나타내는 규칙을 생성합니다.
In[1]:=
IntegrateMeijerG[f_ g_, {z_, 0, Infinity}] /; FreeQ[{f, g}, MeijerG] :=
IntegrateMeijerG[
MeijerGReduce[f, z] MeijerGReduce[g, z], {z, 0, Infinity}]이 적분은 정확히 하나의 MeijerG 식으로 나타낼 수 있습니다.
In[2]:=
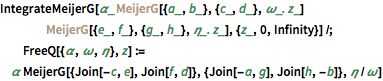
IntegrateMeijerG[\[Alpha]_ Inactive[MeijerG][{a_, b_}, {c_,
d_}, \[Omega]_. z_] Inactive[MeijerG][{e_, f_}, {g_,
h_}, \[Eta]_. z_], {z_, 0, Infinity}] /;
FreeQ[{\[Alpha], \[Omega], \[Eta]},
z] := \[Alpha] MeijerG[{Join[-c, e], Join[f, d]}, {Join[-a, g],
Join[h, -b]}, \[Eta]/\[Omega]]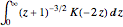 를 평가하는 체계를 적용합니다.
를 평가하는 체계를 적용합니다.
In[3]:=
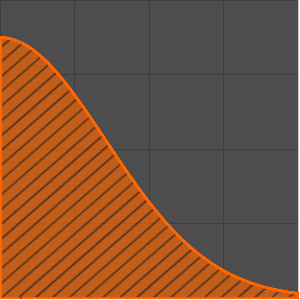
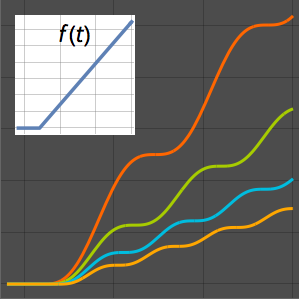
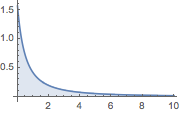
Plot[(1 + z)^(-3/2) EllipticK[-2 z], {z, 0, 10}, Filling -> Axis,
PlotRange -> All]Out[3]=
In[4]:=
IntegrateMeijerG[(1 + z)^(-3/2) EllipticK[-2 z], {z, 0, Infinity}]Out[4]=
Integrate을 사용하여 동일한 결과를 얻습니다.
In[5]:=
Integrate[(1 + z)^(-3/2) EllipticK[-2 z], {z, 0, Infinity}]Out[5]=
답은 완전히 다른 것처럼 보이지만 실제로는 동일합니다.
In[6]:=
IntegrateMeijerG[(1 + z)^(-3/2) EllipticK[-2 z], {z, 0, Infinity}];
Integrate[(1 + z)^(-3/2) EllipticK[-2 z], {z, 0, Infinity}];
FullSimplify[% == %%]Out[6]=