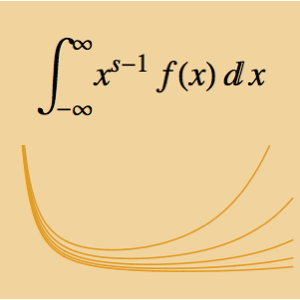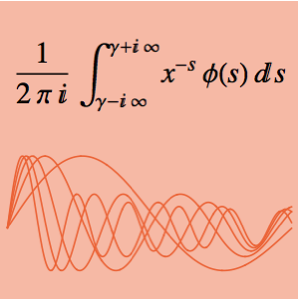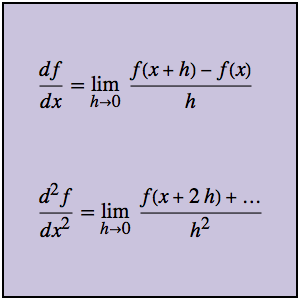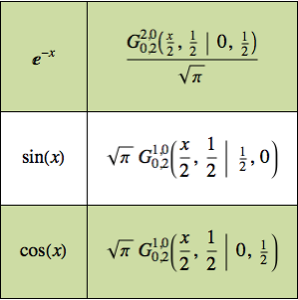用 G 约化计算定积分

将函数表示为 MeijerG 的形式使我们能够计算其在正实数上的乘积.

创建将函数乘积的积分表示为 MeijerG 形式的规则.

In[1]:=

IntegrateMeijerG[f_ g_, {z_, 0, Infinity}] /; FreeQ[{f, g}, MeijerG] := IntegrateMeijerG[ MeijerGReduce[f, z] MeijerGReduce[g, z], {z, 0, Infinity}]

可以用单独的 MeijerG 表达式的形式来精确表示该积分.

In[2]:=

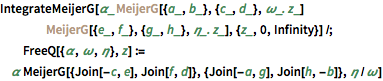
IntegrateMeijerG[\[Alpha]_ Inactive[MeijerG][{a_, b_}, {c_, d_}, \[Omega]_. z_] Inactive[MeijerG][{e_, f_}, {g_, h_}, \[Eta]_. z_], {z_, 0, Infinity}] /; FreeQ[{\[Alpha], \[Omega], \[Eta]}, z] := \[Alpha] MeijerG[{Join[-c, e], Join[f, d]}, {Join[-a, g], Join[h, -b]}, \[Eta]/\[Omega]]

将这个方法应用于计算 .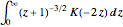

In[3]:=

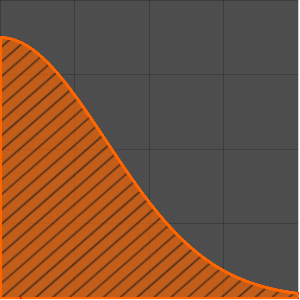
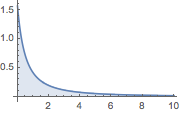
Plot[(1 + z)^(-3/2) EllipticK[-2 z], {z, 0, 10}, Filling -> Axis, PlotRange -> All]

Out[3]=

In[4]:=

IntegrateMeijerG[(1 + z)^(-3/2) EllipticK[-2 z], {z, 0, Infinity}]

Out[4]=

用 Integrate 得到相同的结果.

In[5]:=

Integrate[(1 + z)^(-3/2) EllipticK[-2 z], {z, 0, Infinity}]

Out[5]=

答案虽然看起来很不一样，但它们是等价的.

In[6]:=

IntegrateMeijerG[(1 + z)^(-3/2) EllipticK[-2 z], {z, 0, Infinity}]; Integrate[(1 + z)^(-3/2) EllipticK[-2 z], {z, 0, Infinity}]; FullSimplify[% == %%]

Out[6]=