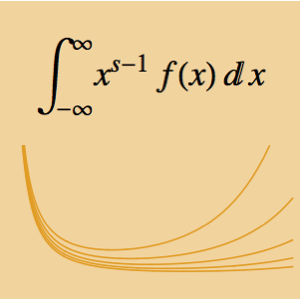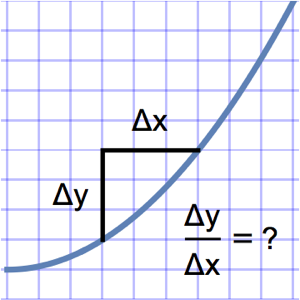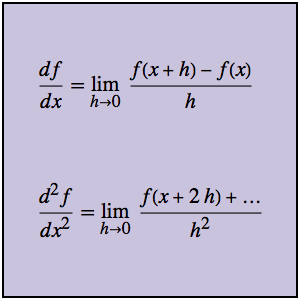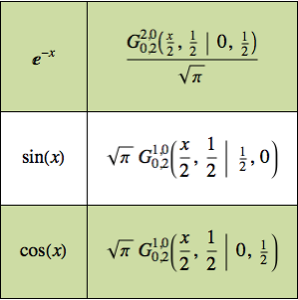Encontre a distribuição de carga em uma esfera

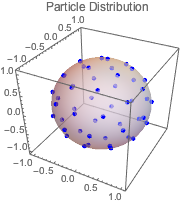
Encontre as posições que maximizam o potencial de Coulomb para que partículas igualmente carregadas possam mover-se livres em uma esfera. Esta é a distribuição de carga de equilíbrio.

Determine por n o número de partículas.

In[1]:=

n = 50;

Deixe que {x_i, y_i, z_i} sejam as coordenadas cartesianas da partícula .

In[2]:=

vars = Join[Array[x, n], Array[y, n], Array[z, n]];

A meta é maximizar o potencial de Coulomb.

In[3]:=

potential = Sum[((x[i] - x[j])^2 + (y[i] - y[j])^2 + (z[i] - z[j])^2)^-(1/ 2), {i, 1, n - 1}, {j, i + 1, n}];

Como as partículas estão na esfera, suas coordenadas devem satisfazer as restrições da magnitude de unidade.

In[4]:=

sphereconstr = Table[x[i]^2 + y[i]^2 + z[i]^2 == 1, {i, 1, n}];

Escolha pontos iniciais na esfera aleatóriamente usando coordenadas esféricas.

In[5]:=

rpts = ConstantArray[1, n]; thetapts = RandomReal[{0, Pi}, n]; phipts = RandomReal[{-Pi, Pi}, n]; spherpts = Transpose[{rpts, thetapts, phipts}];

Transforme os pontos iniciais em coordenadas cartesianas.

In[6]:=

cartpts = CoordinateTransform["Spherical" -> "Cartesian", spherpts];

Reordene os pontos iniciais para que correspondam com a ordem das variáveis.

In[7]:=

initpts = Flatten[Transpose[cartpts]];

Minimize o potencial de Coulomb sujeito à restrição esférica.

In[8]:=

sol = FindMinimum[{potential, sphereconstr}, Thread[{vars, initpts}]];

Extraia da solução as posições de equilíbrio das partículas.

In[9]:=

solpts = Table[{x[i], y[i], z[i]}, {i, 1, n}] /. sol[[2]];

Faça uma representação gráfica do resultado.

In[10]:=

Show[ListPointPlot3D[solpts, PlotRange -> {{-1.1, 1.1}, {-1.1, 1.1}, {-1.1, 1.1}}, PlotStyle -> {{PointSize[.03], Blue}}, AspectRatio -> 1, BoxRatios -> 1, PlotLabel -> "Particle Distribution"], Graphics3D[{Opacity[.5], Sphere[]}]]

Out[10]=