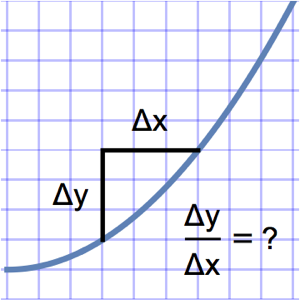Find the Charge Distribution on a Sphere: New in Wolfram Language 11

Find the Charge Distribution on a Sphere

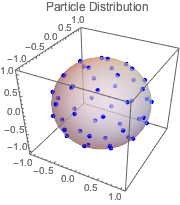
Find the positions that minimize the Coulomb potential for equally charged particles free to move on a sphere. This is the equilibrium charge distribution.

Denote by n the number of particles.

In[1]:=

n = 50;

Let 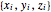be the Cartesian coordinates of the particle.

In[2]:=

vars = Join[Array[x, n], Array[y, n], Array[z, n]];

The goal is to minimize the Coulomb potential.

In[3]:=

potential = 
  Sum[((x[i] - x[j])^2 + (y[i] - y[j])^2 + (z[i] - z[j])^2)^-(1/
       2), {i, 1, n - 1}, {j, i + 1, n}];

Since the particles are on a sphere, their coordinates must satisfy unit-magnitude constraints.

In[4]:=

sphereconstr = Table[x[i]^2 + y[i]^2 + z[i]^2 == 1, {i, 1, n}];

Choose initial points on the sphere at random using spherical coordinates.

In[5]:=

rpts = ConstantArray[1, n];
thetapts = RandomReal[{0, Pi}, n];
phipts = RandomReal[{-Pi, Pi}, n];
spherpts = Transpose[{rpts, thetapts, phipts}];

Transform the initial points to Cartesian coordinates.

In[6]:=

cartpts = CoordinateTransform["Spherical" -> "Cartesian", spherpts];

Rearrange the initial points to match the variables' ordering.

In[7]:=

initpts = Flatten[Transpose[cartpts]];

Minimize the Coulomb potential subject to the sphere constraint.

In[8]:=

sol = FindMinimum[{potential, sphereconstr}, Thread[{vars, initpts}]];

Extract from the solution the equilibrium positions of the particles.

In[9]:=

solpts = Table[{x[i], y[i], z[i]}, {i, 1, n}] /. sol[[2]];

Plot the result.

In[10]:=

Show[ListPointPlot3D[solpts, 
  PlotRange -> {{-1.1, 1.1}, {-1.1, 1.1}, {-1.1, 1.1}}, 
  PlotStyle -> {{PointSize[.03], Blue}}, AspectRatio -> 1, 
  BoxRatios -> 1, PlotLabel -> "Particle Distribution"], 
 Graphics3D[{Opacity[.5], Sphere[]}]]

Out[10]=