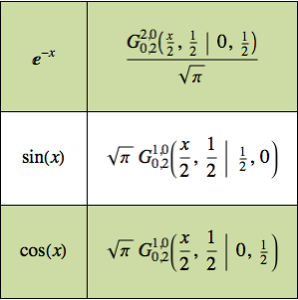구면상의 전하 분포 찾기: Wolfram Language 11의 신기능

‹›

구면상의 전하 분포 찾기

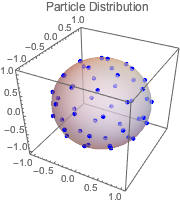
구체 위를 자유롭게 이동하는 등전하 입자의 쿨롱 (Coulomb) 가능성을 최소화하는 위치를 구합니다. 이것은 평형 전하 분포입니다.

입자의 수를 n으로 나타냅니다.

In[1]:=

n = 50;

{x_i, y_i, z_i}를 번째 입자의 직교 좌표로 합니다.

In[2]:=

vars = Join[Array[x, n], Array[y, n], Array[z, n]];

목표는 쿨롱 포텐셜을 최소화하는 것입니다.

In[3]:=

potential = 
  Sum[((x[i] - x[j])^2 + (y[i] - y[j])^2 + (z[i] - z[j])^2)^-(1/
       2), {i, 1, n - 1}, {j, i + 1, n}];

입자는 구면 위에 있기 때문에, 그 좌표는 1이라는 제약 조건을 만족해야 합니다.

In[4]:=

sphereconstr = Table[x[i]^2 + y[i]^2 + z[i]^2 == 1, {i, 1, n}];

구면 좌표계를 사용하여 구면의 초기점을 무작위로 선택합니다.

In[5]:=

rpts = ConstantArray[1, n];
thetapts = RandomReal[{0, Pi}, n];
phipts = RandomReal[{-Pi, Pi}, n];
spherpts = Transpose[{rpts, thetapts, phipts}];

초기점을 직교 좌표로 변환합니다.

In[6]:=

cartpts = CoordinateTransform["Spherical" -> "Cartesian", spherpts];

변수의 순서와 일치하도록 초기점을 정렬합니다.

In[7]:=

initpts = Flatten[Transpose[cartpts]];

구면의 제약 조건의 대상이 되는 쿨롱 포텐셜을 최소화합니다.

In[8]:=

sol = FindMinimum[{potential, sphereconstr}, Thread[{vars, initpts}]];

입자의 평형 위치를 해로부터 추출합니다.

In[9]:=

solpts = Table[{x[i], y[i], z[i]}, {i, 1, n}] /. sol[[2]];

결과를 플롯합니다.

In[10]:=

Show[ListPointPlot3D[solpts, 
  PlotRange -> {{-1.1, 1.1}, {-1.1, 1.1}, {-1.1, 1.1}}, 
  PlotStyle -> {{PointSize[.03], Blue}}, AspectRatio -> 1, 
  BoxRatios -> 1, PlotLabel -> "Particle Distribution"], 
 Graphics3D[{Opacity[.5], Sphere[]}]]

Out[10]=

Wolfram 언어™

구면상의 전하 분포 찾기

관련 예제