Optimize the Shape of a Cam
Design the shape of a convex cam to maximize the area of the valve opening for one rotation of the cam, with constraints on the radii of the cam.
Assume that the shape of the cam is circular over an angle of 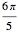 of its circumference with radius
of its circumference with radius 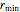 and is shaped symmetrically over the remaining
and is shaped symmetrically over the remaining 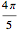 .
.
The design variables 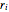 ,
, 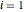 ,
, 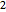 ,
,  ,
,  , represent the radius of the cam at equally spaced angles
, represent the radius of the cam at equally spaced angles 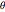 distributed over an angle of
distributed over an angle of 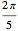 , the top half of the non-circular part of the cam.
, the top half of the non-circular part of the cam.
n = 100; vars = Array[r, n];Each radius 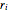 is constrained to lie in the interval
is constrained to lie in the interval 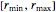 .
.
rmin = 1; rmax = 2;
varbounds = Table[rmin <= r[i] <= rmax, {i, 1, n}];Enter the angle 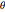 defined above.
defined above.
\[Theta] = 2 Pi/(5 (n + 1));Convexity constraints are expressed by the system of inequalities  .
.
convexconstri = (1/2) r[i - 1] r[i + 1] Sin[2 \[Theta]] <=
(1/2) r[i - 1] r[i] Sin[\[Theta]] + (1/2) r[i] r[
i + 1] Sin[\[Theta]];Using that 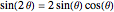 , the system can be re-expressed as follows. Notice that
, the system can be re-expressed as follows. Notice that 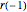 is the radius of a point on the circular part of the cam and hence equal to
is the radius of a point on the circular part of the cam and hence equal to 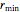 .
.
convexconstr =
Table[2 r[i - 1] r[i + 1] Cos[\[Theta]] <=
r[i] (r[i - 1] + r[i + 1]), {i, 0, n}] /. {r[-1] -> rmin,
r[0] -> rmin, r[n + 1] -> rmax};A constraint on the rate of change of the radius is expressed in terms of the parameter 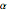 as
as 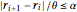 .
.

\[Alpha] = 1.5; rchangeconstr =
Table[-\[Alpha] <= (r[i + 1] - r[i])/\[Theta] <= \[Alpha], {i, 0,
n}] /. {r[0] -> rmin, r[n + 1] -> rmax};The objective function (valve opening area), is assumed to have a simple linear relationship with the design variables 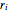 given as
given as 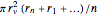 , where
, where 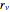 is a constant related to the geometry of the valve.
is a constant related to the geometry of the valve.
rv = 1;
objfun = Pi rv^2 (1/n) Sum[r[i], {i, 1, n}];Choose initial points for the variables.
initpts = Table[.5 (rmin + rmax), {i, 1, n}];Solve the maximization problem.
sol = FindMaximum[
Join[{objfun}, varbounds, convexconstr, rchangeconstr],
Thread[vars, initpts]];Note that several of the largest radii are at the maximum 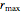 .
.
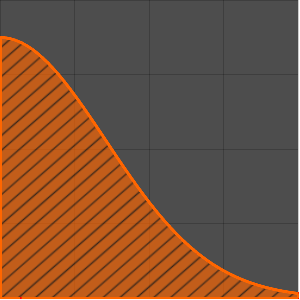
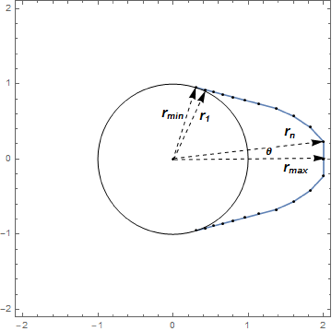
Table[r[i], {i, 95, 100}] /. sol[[2]]Plot the solution.