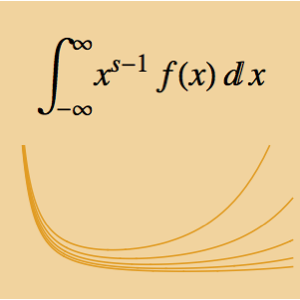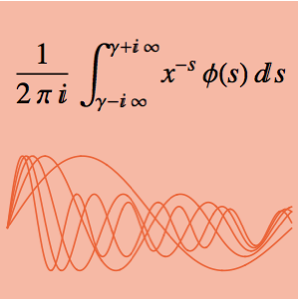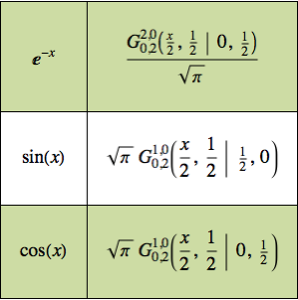Effectuez une convolution de Mellin
Effectuez une convolution de deux fonctions de Mellin en utilisant MellinConvolve.
In[1]:=
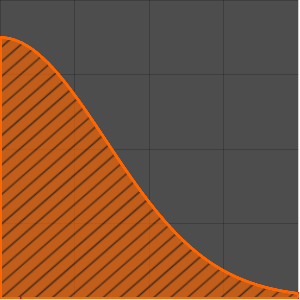
MellinConvolve[UnitBox[x - 3/2], 2 UnitBox[x - 2], x, y]Out[1]=
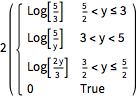
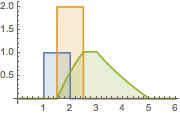
Tracez le résultat avec les fonctions originales.
In[2]:=
MellinConvolve[UnitBox[x - 3/2], 2 UnitBox[x - 2], x, y];
Plot[{UnitBox[y - 3/2], 2 UnitBox[y - 2], %} // Evaluate, {y, 0, 6},
Filling -> Axis, Exclusions -> None, PlotRange -> All]Out[2]=
Effectuez une convolution de Mellin de deux fonctions de Bessel.
In[3]:=
MellinConvolve[BesselJ[0, x], BesselJ[1, x], x, y]Out[3]=
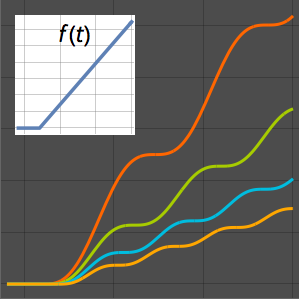
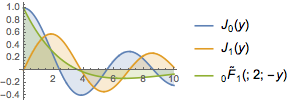
Tracez le résultat avec les fonctions originales.
In[4]:=
MellinConvolve[BesselJ[0, x], BesselJ[1, x], x, y];
Plot[{BesselJ[0, y], BesselJ[1, y], %} // Evaluate, {y, 0, 10},
Filling -> Axis, PlotLegends -> "Expressions"]Out[4]=
Effectuez une convolution de Mellin multivariée.
In[5]:=
MellinConvolve[3 UnitBox[s - 3/2, t - 7/4],
2 UnitBox[s - 1, t - 1], {s, t}, {m, n}]Out[5]=
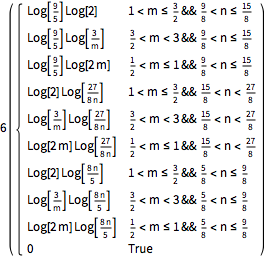
Tracez le résultat avec les fonctions originales.
In[6]:=

MellinConvolve[3 UnitBox[s - 3/2, t - 7/4],
2 UnitBox[s - 1, t - 1], {s, t}, {m, n}];
Plot3D[{3 UnitBox[m - 3/2, n - 7/4], 2 UnitBox[m - 1, n - 1], %} //
Evaluate, {m, 0, 3}, {n, 0, 3}, PlotRange -> All, Filling -> Axis,
PlotPoints -> 50, Exclusions -> None, PlotStyle -> Opacity[0.4],
Ticks -> None, Mesh -> None]Out[6]=