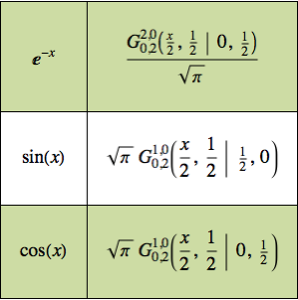Résolvez un problème de valeur initiale en utilisant la fonction de Solve Green: Nouveautés de Wolfram Language 11

Résolvez un problème de valeur initiale en utilisant la fonction de Solve Green

Résolvez un problème de valeur initiale pour une équation différentielle inhomogène en utilisant GreenFunction.

En premier lieu, calculez la fonction de Green.

In[1]:=

gf[s_, t_] = 
 GreenFunction[{-u''[t] + u'[t] - 37/4 u[t], u[0] == 0, u'[0] == 0}, 
  u[t], {t, 0, \[Infinity]}, s]

Out[1]=

Définissez une fonction de forçage.

In[2]:=

f[t_] := Cos[a t]

Avec la convolution de la fonction de Green Avec la fonction de forçage on obtient la solution.

In[3]:=

sol = Integrate[gf[s, t] f[s], {s, 0, \[Infinity]}, 
  Assumptions -> t > 0]

Out[3]=

Comparez avec le résultat donné par DSolveValue.

In[4]:=

DSolveValue[{-u''[t] + u'[t] - 37/4 u[t] == f[t], u[0] == 0, 
   u'[0] == 0}, u[t], t] // FullSimplify

Out[4]=

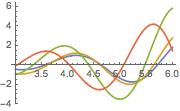
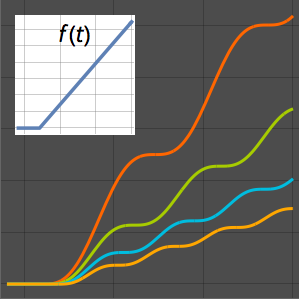
Tracez la solution pour différentes valeurs du paramètre .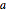

In[5]:=

Plot[Table[sol, {a, 1, 4, 0.8}] // Evaluate, {t, 3, 6}]

Out[5]=