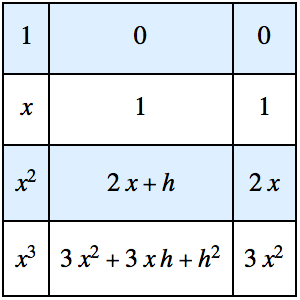
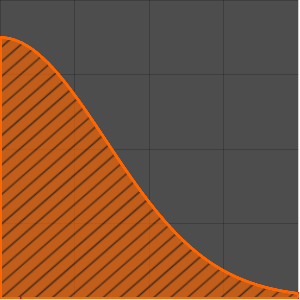
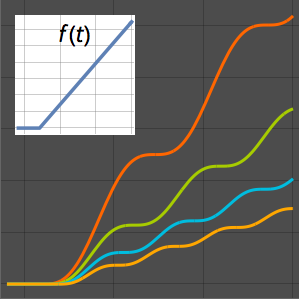
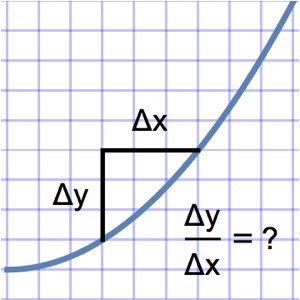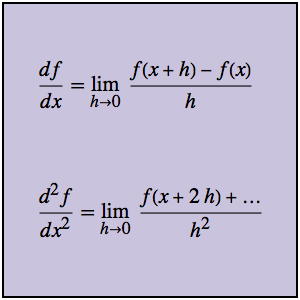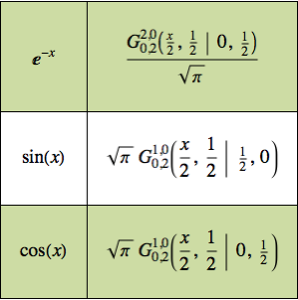Optimisez la forme d'une came

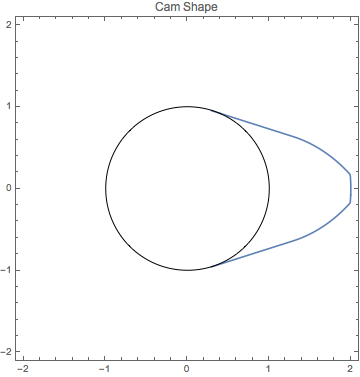
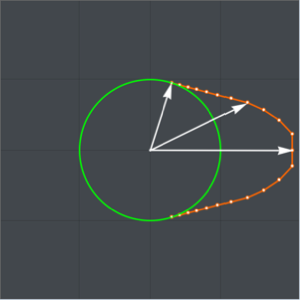
Dessinez la forme d'une came convexe pour maximiser la zone de l'ouverture de la vanne pour une rotation de la came, avec des contraintes sur les rayons de la came.

Supposons que la forme de la came soit circulaire sur un angle de 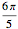de sa circonférence 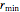avec un rayon 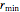et est de forme symétrique sur le reste .

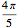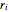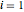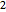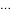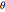Les variables de conception , , , , , représentent le rayon de la came aux angles équidistants distribués sur un angle de 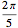, la moitié supérieure de la partie non circulaire de la came.

In[1]:=

n = 100; vars = Array[r, n];

Chaque rayon 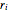est contraint de tomber dans l'intervalle .

In[2]:=

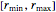rmin = 1; rmax = 2; varbounds = Table[rmin <= r[i] <= rmax, {i, 1, n}];

Entrez l'angle 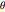défini ci-dessus.

In[3]:=

\[Theta] = 2 Pi/(5 (n + 1));

Les contraintes de convexité sont exprimées par le système des inégalités.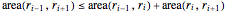

In[4]:=

convexconstri = (1/2) r[i - 1] r[i + 1] Sin[2 \[Theta]] <= (1/2) r[i - 1] r[i] Sin[\[Theta]] + (1/2) r[i] r[ i + 1] Sin[\[Theta]];

En utilisant 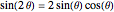, le système peut être réexprimé comme suit. Notez que 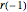est le rayon du point sur la partie circulaire de la came et est donc égal à .

In[5]:=

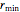convexconstr = Table[2 r[i - 1] r[i + 1] Cos[\[Theta]] <= r[i] (r[i - 1] + r[i + 1]), {i, 0, n}] /. {r[-1] -> rmin, r[0] -> rmin, r[n + 1] -> rmax};

Une contrainte sur le taux de variation du rayon est exprimé en termes du paramètre 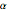comme .

In[6]:=

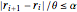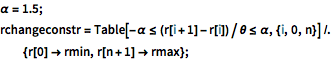
\[Alpha] = 1.5; rchangeconstr = Table[-\[Alpha] <= (r[i + 1] - r[i])/\[Theta] <= \[Alpha], {i, 0, n}] /. {r[0] -> rmin, r[n + 1] -> rmax};

La fonction objective (aire d'ouverture de la vanne), est supposée avoir une relation linéaire simple avec les variable de conception 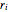donné comme 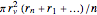, où 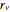est une constante liée à la géométrie de la vanne.

In[7]:=

rv = 1; objfun = Pi rv^2 (1/n) Sum[r[i], {i, 1, n}];

Choisissez les points initiaux pour les variables.

In[8]:=

initpts = Table[.5 (rmin + rmax), {i, 1, n}];

Résolvez le problème de maximisation.

In[9]:=

sol = FindMaximum[ Join[{objfun}, varbounds, convexconstr, rchangeconstr], Thread[vars, initpts]];

Notez que plusieurs des plus grands rayons sont au maximum .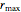

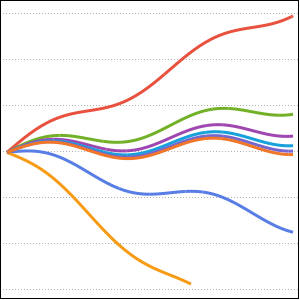
In[10]:=

Table[r[i], {i, 95, 100}] /. sol[[2]]

Out[10]=

Tracez la solution.

In[11]:=

solpts1 = Table[{r[i] Cos[-2. Pi/5 + \[Theta] i], r[i] Sin[-2. Pi/5. + \[Theta] i]}, {i, -1, n + 2}] /. {r[-1] -> rmin, r[0] -> rmin, r[n + 1] -> rmax, r[n + 2] -> r[n]} /. sol[[2]]; solpts2 = Map[{#[[1]], -#[[2]]} &, Reverse@solpts1]; solpts = Join[solpts1, solpts2]; Show[ListLinePlot[solpts, PlotRange -> {{-2.1, 2.1}, {-2.1, 2.1}}, PlotLabel -> "Cam Shape", AspectRatio -> 1, Axes -> False, Frame -> True], Graphics[{Circle[{0., 0.}, 1.]}], ImageSize -> Medium]

Out[11]=