Résolvez le problème du tautochrone
Le problème du tautochrone consiste à trouver la courbe le long de laquelle une perle placée n'importe où tombera vers le bas pendant le même laps de temps. En exprimant le temps de chute total en fonction de la longueur de l'arc de la courbe et de la vitesse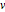 
, on obtient l'équation intégrale d'Abel 
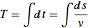. Le fait de définir la fonction inconnue 
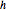par la relation 
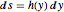et en utilisant la conservation de l'équation de l'énergie 
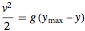donne l'équation explicite suivante.
abeleqn = T == 1/Sqrt[2 g] \!\(
\*SubsuperscriptBox[\(\[Integral]\), \(0\), \(y\)]\(
\*FractionBox[\(h[z]\),
SqrtBox[\(y - z\)]] \[DifferentialD]z\)\);Utilisez DSolveValue pour résoudre l'équation d'intégrale.
dsdy = DSolveValue[abeleqn, h[y], y]
En utilisant la relation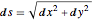 
, résolvez pour 
.
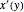dxdy = Sqrt[dsdy^2 - 1]
En commençant la courbe par l'origine et en l'intégrant, on obtient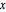 
en tant que fonction de 
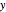. Remarquez que les hypothèses garantissent que l'intégrande est à valeur réelle.
x[y_] = Integrate[dxdy, {y, 0, y},
Assumptions -> (2 g (T^2) )/(\[Pi]^2 y) > 1 && y > 0]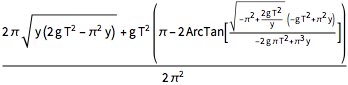
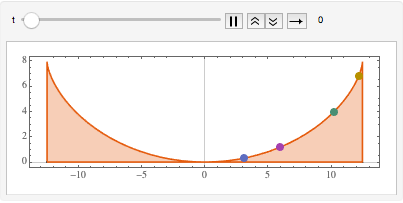
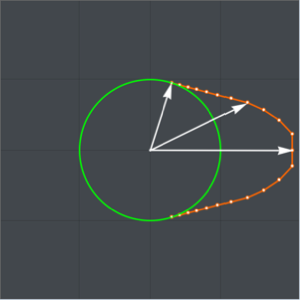
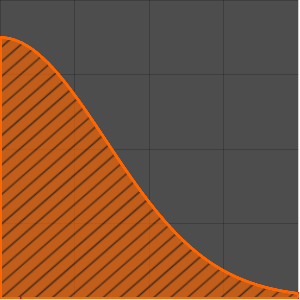
En utilisant un temps de descente de deux secondes et en substituant la valeur de l'accélération gravitationnelle, tracez la courbe maximale du tautochrone. (La branche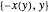 
vient de la solution 
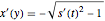pour la dérivée de 
.)
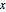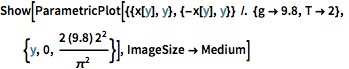
Show[ParametricPlot[{{x[y], y}, {-x[y], y}} /. {g -> 9.8, T -> 2}, {y,
0, (2 (9.8) 2^2)/\[Pi]^2}], ImageSize -> Medium]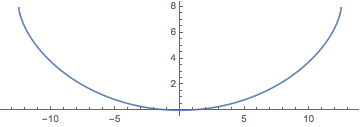
Le fait de changer les variables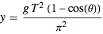 
donne une paramétrisation simple et non singulière de la courbe avec 
.
c[\[Theta]_] = (
g T^2)/\[Pi]^2 {Sin[\[Theta]] + \[Theta], 1 - Cos[\[Theta]]} ;Le fait de combiner la conservation de l'équation d'énergie et la règle de la chaîne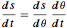 
produit l'équation différentielle suivante pour 
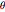en tant que fonction de 
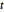qui peut être résolue numériquement.
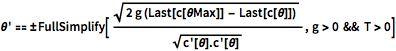
\[Theta]' == \[PlusMinus]FullSimplify[ Sqrt[
2 g (Last[c[\[Theta]Max]] - Last[c[\[Theta]]])] /Sqrt[
c'[\[Theta]].c'[\[Theta]]] , g > 0 && T > 0]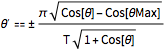
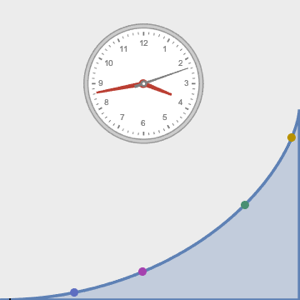
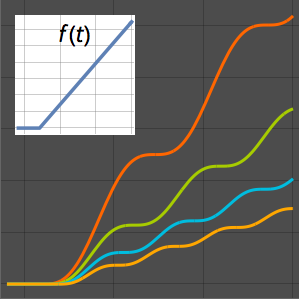
Visualisez le mouvement le long du tautochrone.
