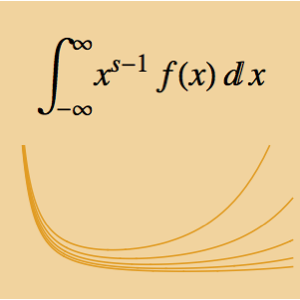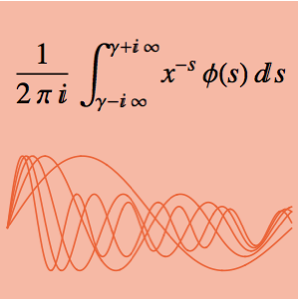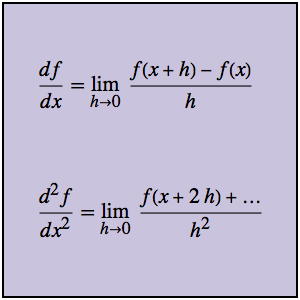Évaluez une dérivée en utilisant les premiers principes
Les quotients de différence peuvent être utilisés non seulement pour calculer directement la dérivée première, mais aussi les dérivées d'ordre supérieur. Considérez d'abord la fonction g et son quotient de différence associé.
In[1]:=
g[x_] := x^2 Exp[x]In[2]:=
dq1[x_] = DifferenceQuotient[g[x], {x, h}]Out[2]=
En prenant la limite du quotient de la différence, on obtient la dérivée première.
In[3]:=
Limit[dq1[x], h -> 0]Out[3]=
In[4]:=
Limit[dq1[x], h -> 0];
Simplify[% == g'[x]]Out[4]=
La première dérivée peut être calculée directement à partir du deuxième quotient de différence, sans jamais se référer à la première dérivée.
In[5]:=
dq2[x_] = DifferenceQuotient[g[x], {x, 2, h}]Out[5]=
La limite en tant que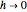 
est la dérivée seconde.
In[6]:=
Limit[dq2[x], h -> 0]Out[6]=
In[7]:=
Limit[dq2[x], h -> 0];
Simplify[% == g''[x]]Out[7]=
Le quotient de différence de la dérivée première est une fonction différente du quotient de différence du second ordre de g, mais sa limite est également la dérivée seconde.
In[8]:=
dqp[x_] = DifferenceQuotient[g'[x], {x, h}]Out[8]=
In[9]:=
Limit[dqp[x], h -> 0]Out[9]=
