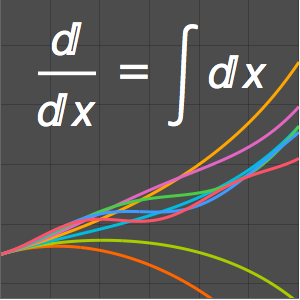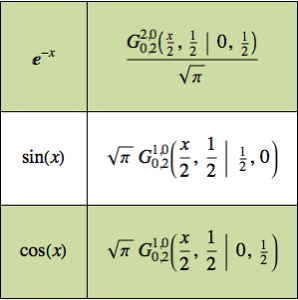グリーン関数を使って境界値問題を解く
指定された斉時境界条件の対象となる次の二階微分方程式を解く．
In[1]:=
eqn = -u''[x] - u'[x] + 6 u[x] == f[x];In[2]:=
bc0 = u[0] == 0;In[3]:=
bc1 = u[1] == 0;強制項は次の関数 f[x]によって与えられる．
In[4]:=
f[x_] := E^(-a x)対応する微分演算子に対するグリーン関数を計算する．
In[5]:=
gf[y_, x_] = GreenFunction[{eqn[[1]], bc0, bc1}, u[x], {x, 0, 1}, y]Out[5]=
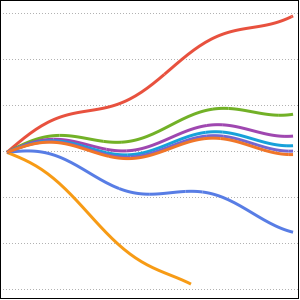
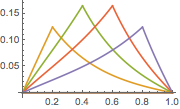
0から1の間にある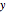 
lのさまざまな値に対するグリーン関数をプロットする．
In[6]:=
Plot[Table[gf[y, x], {y, 0, 1, 0.2}] // Evaluate, {x, 0, 1}]Out[6]=
指定された強制項を持つもとの微分方程式の解は，区間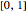
上のたたみ込み積分を使って計算できるようになる．
In[7]:=
sol = Integrate[gf[y, x] f[y], {y, 0, 1}, Assumptions -> 0 < x < 1] //
SimplifyOut[7]=
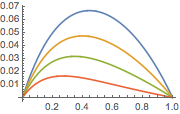
パラメータ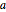 
のさまざまな値に対する解をプロットする．
In[8]:=
Plot[Table[sol, {a, {1/4, 1, 2, 4}}] // Evaluate, {x, 0, 1}]Out[8]=
