用格林函数解边界值问题
求解下面满足给定齐次边界条件的二阶微分方程.
In[1]:=
eqn = -u''[x] - u'[x] + 6 u[x] == f[x];In[2]:=
bc0 = u[0] == 0;In[3]:=
bc1 = u[1] == 0;外力项由下面的函数 f[x] 给出.
In[4]:=
f[x_] := E^(-a x)计算相应微分算子的格林函数.
In[5]:=
gf[y_, x_] = GreenFunction[{eqn[[1]], bc0, bc1}, u[x], {x, 0, 1}, y]Out[5]=
绘出 
在 0 和 1 之间取不同的值时格林函数的图形.
In[6]:=
Plot[Table[gf[y, x], {y, 0, 1, 0.2}] // Evaluate, {x, 0, 1}]Out[6]=
现在可以用区间 [0,1] 上的卷积来计算具有给定外力项的原微分方程的解.
In[7]:=
sol = Integrate[gf[y, x] f[y], {y, 0, 1}, Assumptions -> 0 < x < 1] //
SimplifyOut[7]=
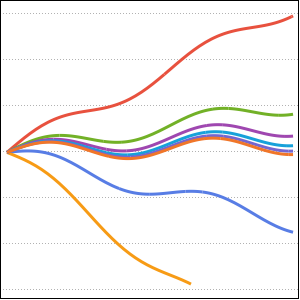
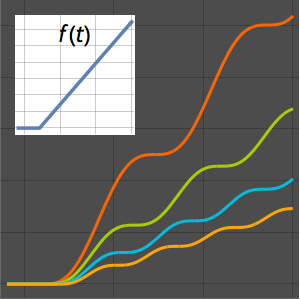
绘制参数 a 取不同值时解的图形.
In[8]:=
Plot[Table[sol, {a, {1/4, 1, 2, 4}}] // Evaluate, {x, 0, 1}]Out[8]=
