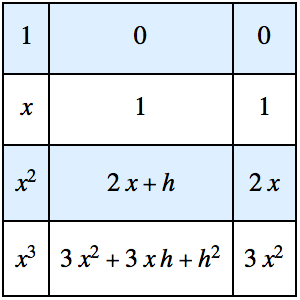
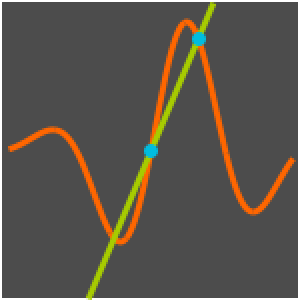
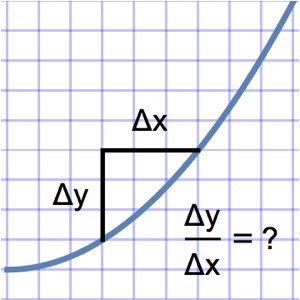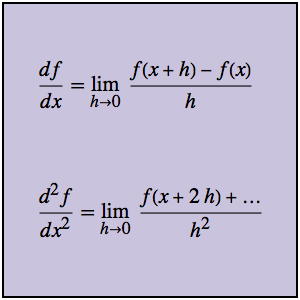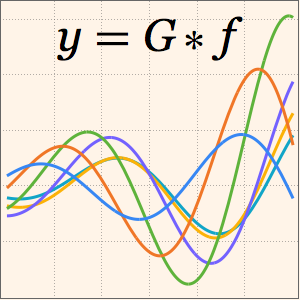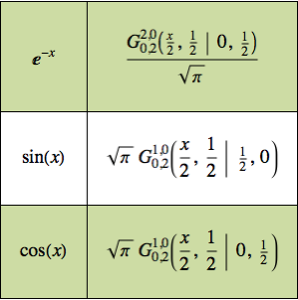Résolvez un problème à valeur de limite avec une fonction de Green
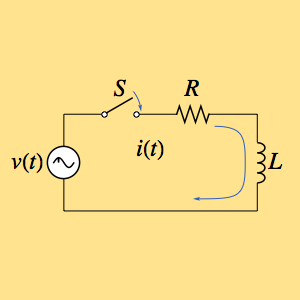
Résolvez l'équation différentielle du second ordre suivante sous réserve des conditions aux limites homogènes données.
In[1]:=
eqn = -u''[x] - u'[x] + 6 u[x] == f[x];In[2]:=
bc0 = u[0] == 0;In[3]:=
bc1 = u[1] == 0;Le terme de forçage est donné par la fonction f[x] suivante.
In[4]:=
f[x_] := E^(-a x)Calculez une fonction de Green pour l'opérateur différentiel correspondant.
In[5]:=
gf[y_, x_] = GreenFunction[{eqn[[1]], bc0, bc1}, u[x], {x, 0, 1}, y]Out[5]=
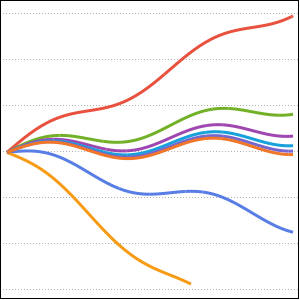
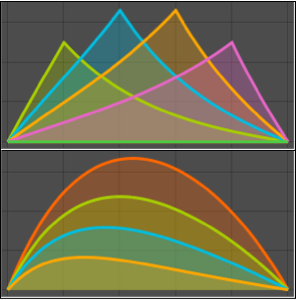
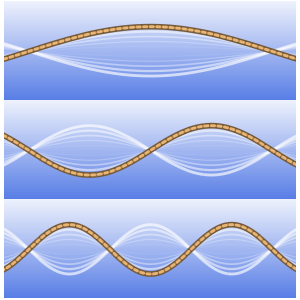
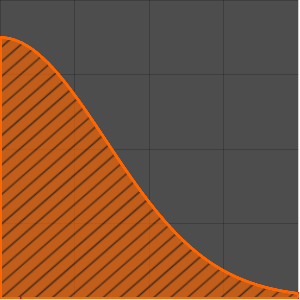
Tracez une fonction de Green pour différentes valeurs de 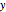 compris entre 0 et 1.
compris entre 0 et 1.
In[6]:=
Plot[Table[gf[y, x], {y, 0, 1, 0.2}] // Evaluate, {x, 0, 1}]Out[6]=
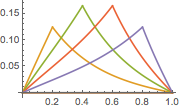
La solution de l'équation différentielle originale avec le terme de forçage donné peut maintenant être calculée en utilisant une intégrale de convolution sur l'intervalle 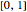 .
.
In[7]:=
sol = Integrate[gf[y, x] f[y], {y, 0, 1}, Assumptions -> 0 < x < 1] //
SimplifyOut[7]=
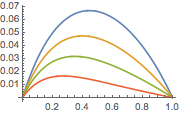
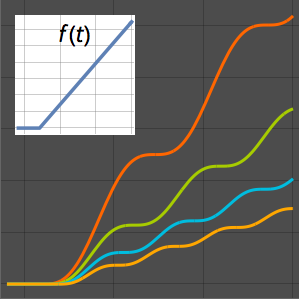
Tracez la solution pour différentes valeurs du paramètre 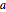 .
.
In[8]:=
Plot[Table[sol, {a, {1/4, 1, 2, 4}}] // Evaluate, {x, 0, 1}]Out[8]=