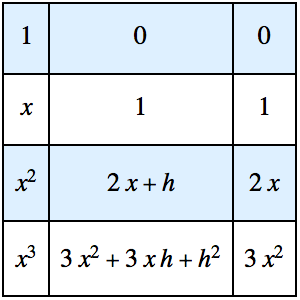
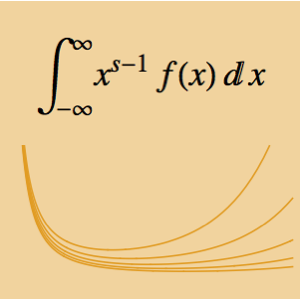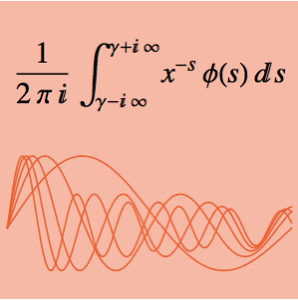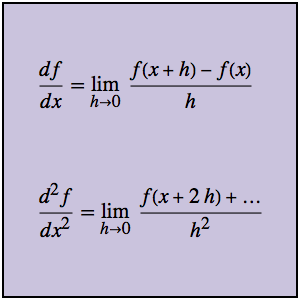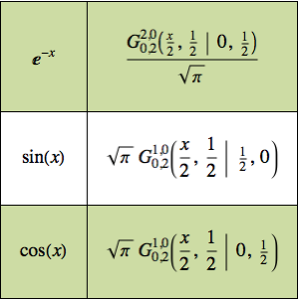Solución de un problema de desafío de SIAM
La integral 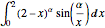 depende del parámetro α. Encuentre el valor de
depende del parámetro α. Encuentre el valor de 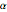 que yace entre
que yace entre 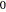 y
y 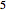 y maximiza la integral. La integral dada puede ser considerada como una convulación de Mellin de dos funciones.
y maximiza la integral. La integral dada puede ser considerada como una convulación de Mellin de dos funciones.
In[1]:=
f[x_] := x (2 - x)^\[Alpha] UnitBox[(x - 1)/2]In[2]:=
g[x_] := Sin[x]Calcule la convolución de Mellin de f[x] y g[x].
In[3]:=
(mc = MellinConvolve[f[x], g[x], x, \[Alpha]]) // TraditionalFormOut[3]//TraditionalForm=
Compare con el resultado dado por Integrate.
In[4]:=
Integrate[(2 - x)^\[Alpha] Sin[\[Alpha]/x], {x, 0, 2},
Assumptions -> \[Alpha] > 0] // TraditionalFormOut[4]//TraditionalForm=
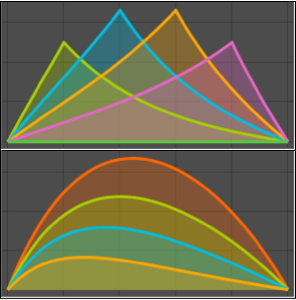
Represente gráficamente la integral como una función de 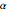 .
.
In[5]:=
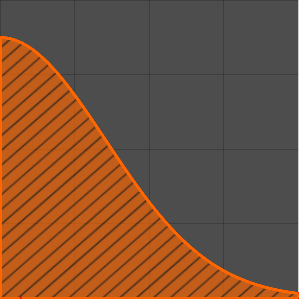
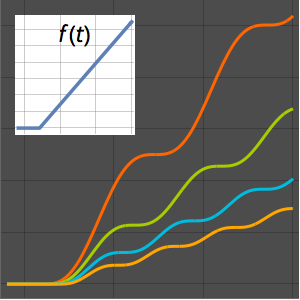
Plot[mc // Evaluate, {\[Alpha], 0, 4.99}, PlotStyle -> Red]Out[5]=
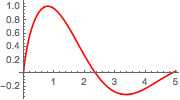
Calcule el argumento que maximice la integral en 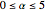 usando FindArgMax.
usando FindArgMax.
In[6]:=
N[FindArgMax[mc, {\[Alpha], 1}, WorkingPrecision -> 100][[1]], 20]Out[6]=