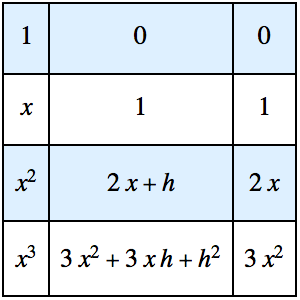
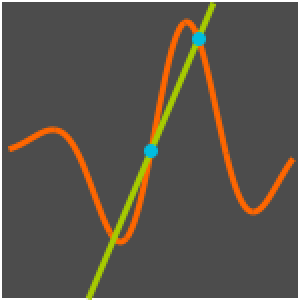
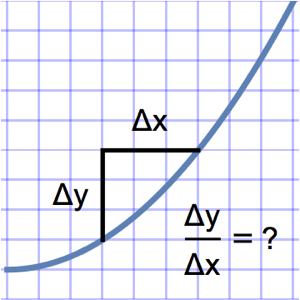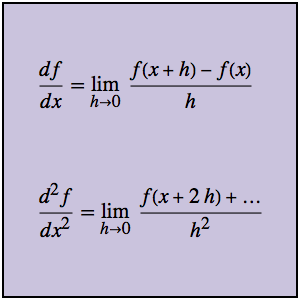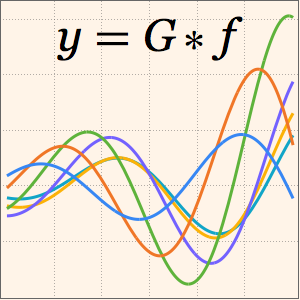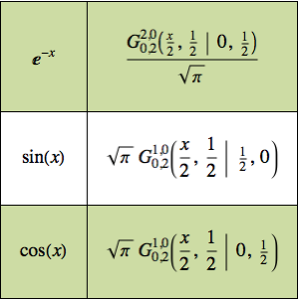Solución de un problema de valor inicial usando la función de Green
Resuelva un problema de valor inicial para una ecuación diferencial no homogénea usando GreenFunction.
Primero calcule la función de Green.
In[1]:=
gf[s_, t_] =
GreenFunction[{-u''[t] + u'[t] - 37/4 u[t], u[0] == 0, u'[0] == 0},
u[t], {t, 0, \[Infinity]}, s]Out[1]=
Defina una función de fuerza.
In[2]:=
f[t_] := Cos[a t]Con la convolución de la función de Green con la función de fuerza se obtiene la solución.
In[3]:=
sol = Integrate[gf[s, t] f[s], {s, 0, \[Infinity]},
Assumptions -> t > 0]Out[3]=
Compare con el resultado dado por DSolveValue.
In[4]:=
DSolveValue[{-u''[t] + u'[t] - 37/4 u[t] == f[t], u[0] == 0,
u'[0] == 0}, u[t], t] // FullSimplifyOut[4]=
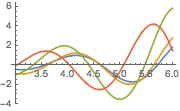
Represente gráficamente la solución para distintos valores del parámetro 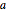 .
.
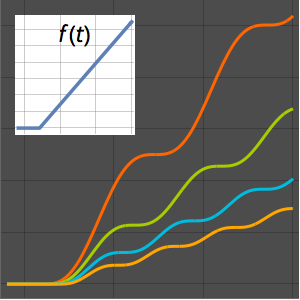
In[5]:=
Plot[Table[sol, {a, 1, 4, 0.8}] // Evaluate, {t, 3, 6}]Out[5]=