Wolfram Language™

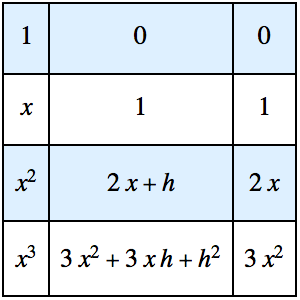
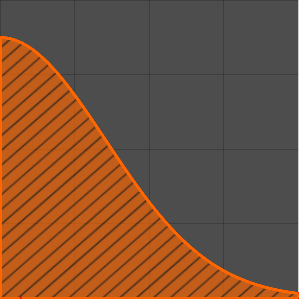
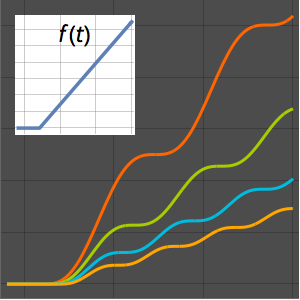
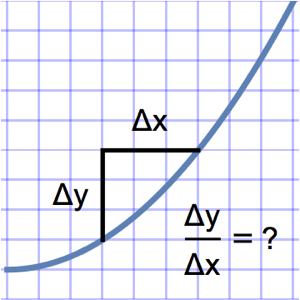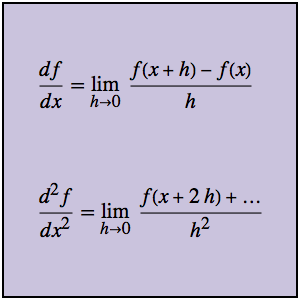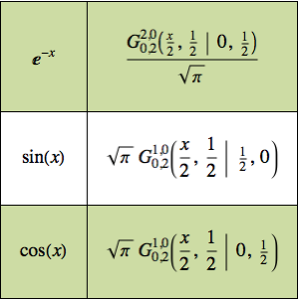Optimización de la forma de una leva

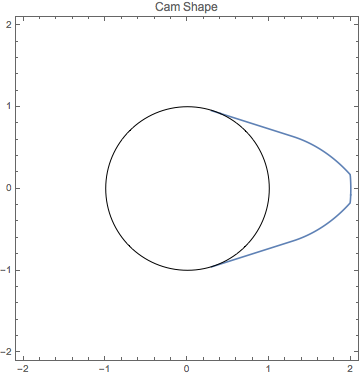
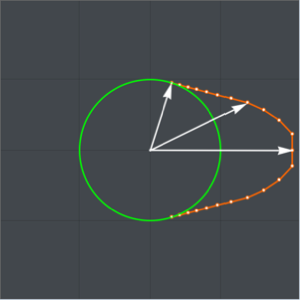
Diseñe la forma de una leva convexa para maximizar el área de la apertura de la válvula para una rotación de la leva, con restricciones en los radios de la leva.

Asuma que la forma de la leva es circular sobre un ángulo de 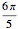de su circunferencia con radio r_min y está formada simétricamente sobre el restante .

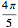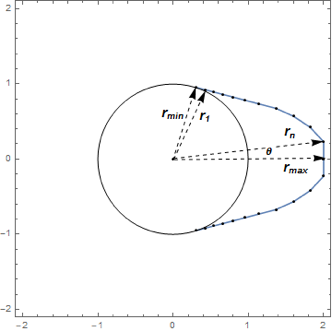
Las variables de diseño 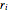, , 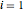, , 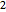, 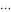representan el radio de la leva en ángulos equidistantes 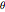distribuidos sobre un ángulo de 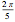, la mitad superior de la parte no circular de la leva.

In[1]:=

n = 100; vars = Array[r, n];

Cada radio 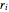está obligado a estar en el intervalo .

In[2]:=

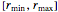rmin = 1; rmax = 2; varbounds = Table[rmin <= r[i] <= rmax, {i, 1, n}];

Ingrese el ángulo 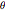definido anteriormente.

In[3]:=

\[Theta] = 2 Pi/(5 (n + 1));

Restricciones a la convexidad son expresadas por el sistema de inequidades .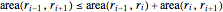

In[4]:=

convexconstri = (1/2) r[i - 1] r[i + 1] Sin[2 \[Theta]] <= (1/2) r[i - 1] r[i] Sin[\[Theta]] + (1/2) r[i] r[ i + 1] Sin[\[Theta]];

Usando 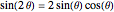, el sistema puede ser expresado de nuevo como sigue. Note que 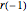es el radio de un punto en la parte circular de la leva y por lo tanto igual a .

In[5]:=

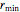convexconstr = Table[2 r[i - 1] r[i + 1] Cos[\[Theta]] <= r[i] (r[i - 1] + r[i + 1]), {i, 0, n}] /. {r[-1] -> rmin, r[0] -> rmin, r[n + 1] -> rmax};

Una restricción en el índice de cambio del radio se expresa en términos del parámetro 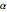como .

In[6]:=

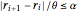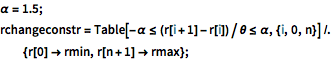
\[Alpha] = 1.5; rchangeconstr = Table[-\[Alpha] <= (r[i + 1] - r[i])/\[Theta] <= \[Alpha], {i, 0, n}] /. {r[0] -> rmin, r[n + 1] -> rmax};

La función objetivo (área de apertura de la válvula), se supone que tiene una relación lineal simple con las variables de diseño 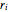dado como 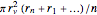, donde 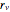es una constante relacionadas con la geometría de la válvula.

In[7]:=

rv = 1; objfun = Pi rv^2 (1/n) Sum[r[i], {i, 1, n}];

Seleccione puntos iniciales para las variables.

In[8]:=

initpts = Table[.5 (rmin + rmax), {i, 1, n}];

Resuelva el problema de maximización.

In[9]:=

sol = FindMaximum[ Join[{objfun}, varbounds, convexconstr, rchangeconstr], Thread[vars, initpts]];

Note que varios de los radios más grandes están en el máximo .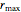

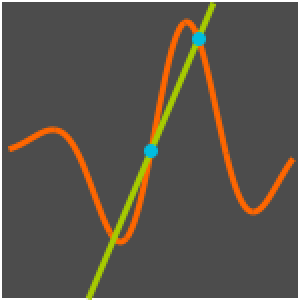
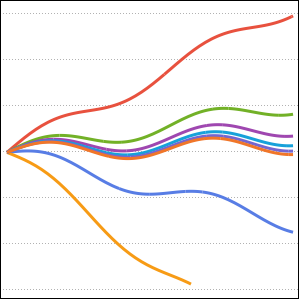
In[10]:=

Table[r[i], {i, 95, 100}] /. sol[[2]]

Out[10]=

Represente gráficamente la solución.

In[11]:=

solpts1 = Table[{r[i] Cos[-2. Pi/5 + \[Theta] i], r[i] Sin[-2. Pi/5. + \[Theta] i]}, {i, -1, n + 2}] /. {r[-1] -> rmin, r[0] -> rmin, r[n + 1] -> rmax, r[n + 2] -> r[n]} /. sol[[2]]; solpts2 = Map[{#[[1]], -#[[2]]} &, Reverse@solpts1]; solpts = Join[solpts1, solpts2]; Show[ListLinePlot[solpts, PlotRange -> {{-2.1, 2.1}, {-2.1, 2.1}}, PlotLabel -> "Cam Shape", AspectRatio -> 1, Axes -> False, Frame -> True], Graphics[{Circle[{0., 0.}, 1.]}], ImageSize -> Medium]

Out[11]=