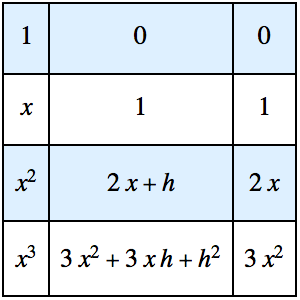
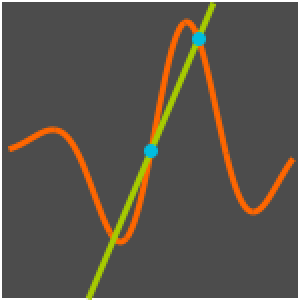
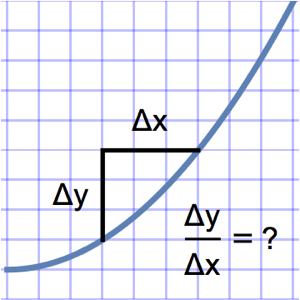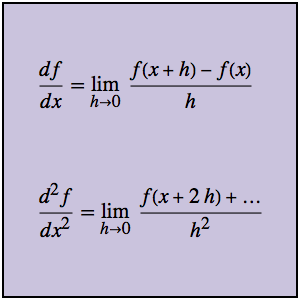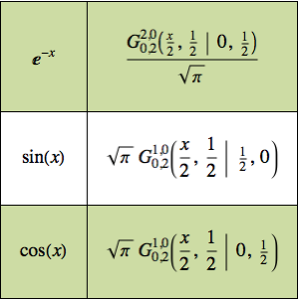Encuentre la respuesta de impulso de un circuito
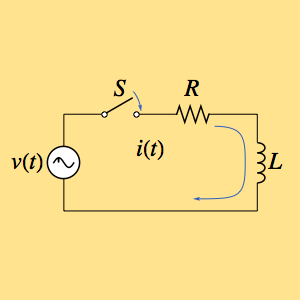
Encuentre la respuesta de impulso para un circuito que está compuesto por una resistencia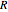 
y un inductor 
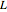, y que es accionado por un voltaje 
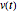dependiente del tiempo.
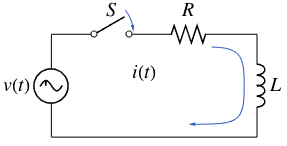
El actual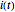 
puede ser calculado resolviendo una ecuación diferencial de primer orden.
Configure el operador diferencial correspondiente a la mano izquierda de la ecuación diferencial ordinaria.
In[1]:=
voltage = L i'[t] + R i[t];Asuma que el interruptor está abierto inicialmente.
In[2]:=
init = i[0] == 0;Calcule la respuesta de impulso para el circuito usando GreenFunction.
In[3]:=
gf[s_, t_] =
GreenFunction[{voltage, init}, i[t], {t, 0, \[Infinity]}, s]Out[3]=
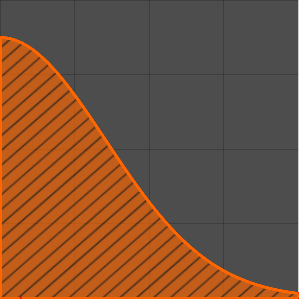
Represente gráficamente la respuesta de impulso en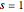 
.
In[4]:=
Plot[gf[s, t] /. {s -> 1, R -> 2, L -> 4}, {t, 0, 7},
PlotTheme -> "Scientific", AxesLabel -> {"t", "i[t]"}]Out[4]=
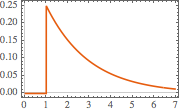
Calcule la respuesta del circuito a un voltaje de paso.
In[5]:=
v[t_] := HeavisideTheta[t];In[6]:=
current = Integrate[gf[s, t] v[s], {s, 0, t}, Assumptions -> t > 0]Out[6]=
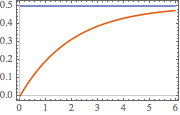
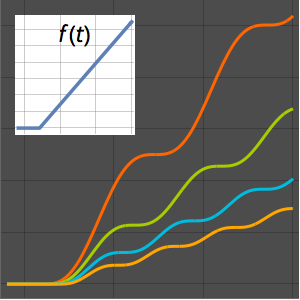
Visualice la respuesta de paso.
In[7]:=
Plot[{current /. {R -> 2, L -> 4}, 0.5} // Evaluate, {t, 0, 6},
PlotTheme -> "Scientific"]Out[7]=
