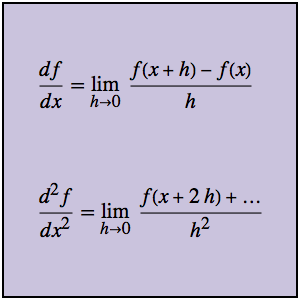Evaluación de una derivada usando primeros principios
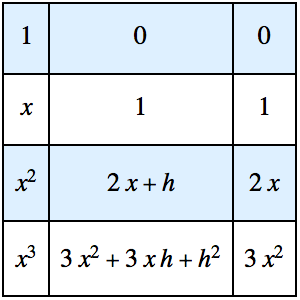
Los cocientes de diferencia pueden ser utilizados directamente para calcular no sólo la primera derivada, sino también derivadas de orden superior. Considere primero la función g y su cociente de diferencia asociado.
In[1]:=
g[x_] := x^2 Exp[x]In[2]:=
dq1[x_] = DifferenceQuotient[g[x], {x, h}]Out[2]=
Tomando el límite del cociente de diferencia de la primera derivada.
In[3]:=
Limit[dq1[x], h -> 0]Out[3]=
In[4]:=
Limit[dq1[x], h -> 0];
Simplify[% == g'[x]]Out[4]=
La segunda derivada puede ser calculada directamente a partir del segundo cociente de diferencia, sin nunca referirse a la primer derivada.
In[5]:=
dq2[x_] = DifferenceQuotient[g[x], {x, 2, h}]Out[5]=
El límite como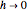 
es la segunda derivada.
In[6]:=
Limit[dq2[x], h -> 0]Out[6]=
In[7]:=
Limit[dq2[x], h -> 0];
Simplify[% == g''[x]]Out[7]=
El cociente de diferencia de la primera derivada es una función distinta del cociente de diferencia de segundo orden de g, pero su límite también es la segunda derivada.
In[8]:=
dqp[x_] = DifferenceQuotient[g'[x], {x, h}]Out[8]=
In[9]:=
Limit[dqp[x], h -> 0]Out[9]=
