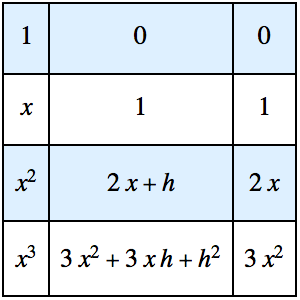
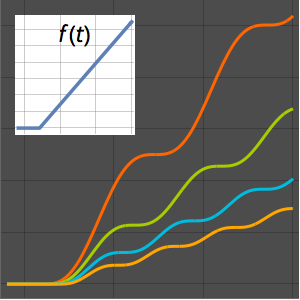
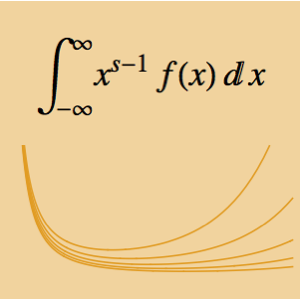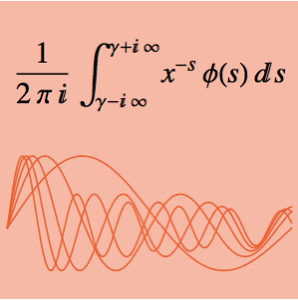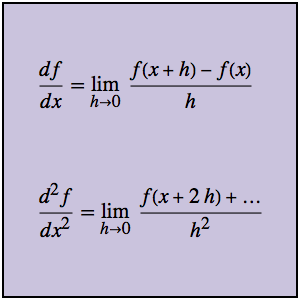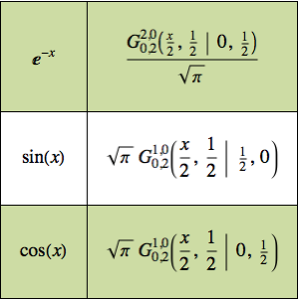Calcule integrales definidas usando reducción G
La expresión de funciones en términos de MeijerG permite el cálculo de su producto sobre reales positivos.
Cree una regla para expresar el integral de un producto de funciones en términos de funciones de MeijerG.
In[1]:=
IntegrateMeijerG[f_ g_, {z_, 0, Infinity}] /; FreeQ[{f, g}, MeijerG] :=
IntegrateMeijerG[
MeijerGReduce[f, z] MeijerGReduce[g, z], {z, 0, Infinity}]Esta integral puede ser expresada exactamente en términos de una única expresión de MeijerG.
In[2]:=
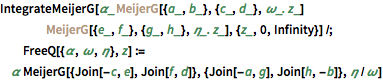
IntegrateMeijerG[\[Alpha]_ Inactive[MeijerG][{a_, b_}, {c_,
d_}, \[Omega]_. z_] Inactive[MeijerG][{e_, f_}, {g_,
h_}, \[Eta]_. z_], {z_, 0, Infinity}] /;
FreeQ[{\[Alpha], \[Omega], \[Eta]},
z] := \[Alpha] MeijerG[{Join[-c, e], Join[f, d]}, {Join[-a, g],
Join[h, -b]}, \[Eta]/\[Omega]]Aplique el esquema para evaluar 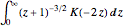 .
.
In[3]:=
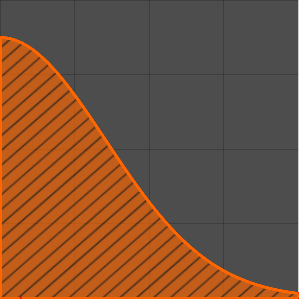
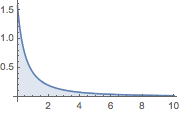
Plot[(1 + z)^(-3/2) EllipticK[-2 z], {z, 0, 10}, Filling -> Axis,
PlotRange -> All]Out[3]=
In[4]:=
IntegrateMeijerG[(1 + z)^(-3/2) EllipticK[-2 z], {z, 0, Infinity}]Out[4]=
Obtenga el mismo resultado usando Integrate.
In[5]:=
Integrate[(1 + z)^(-3/2) EllipticK[-2 z], {z, 0, Infinity}]Out[5]=
A pesar de que la respuesta se ve muy diferente, ésta es equivalente.
In[6]:=
IntegrateMeijerG[(1 + z)^(-3/2) EllipticK[-2 z], {z, 0, Infinity}];
Integrate[(1 + z)^(-3/2) EllipticK[-2 z], {z, 0, Infinity}];
FullSimplify[% == %%]Out[6]=