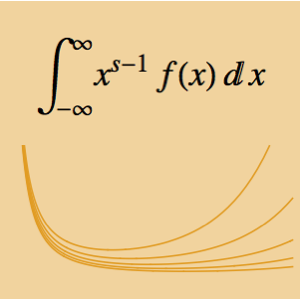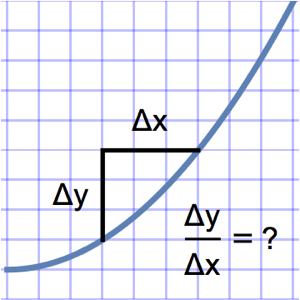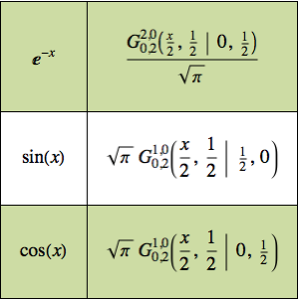Encuentre la distribución de carga en una esfera: Nuevo en Wolfram Language 11

Encuentre la distribución de carga en una esfera

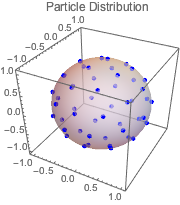
Encuentre las posiciones que minimizan el potencial de Coulomb para que partículas igualmente cargadas puedan moverse libres en una esfera. Esta es la distribución de carga de equilibrio.

Denote con n el número de partículas.

In[1]:=

n = 50;

Permita que 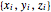sean las coordenadas cartesianas de la partícula.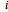

In[2]:=

vars = Join[Array[x, n], Array[y, n], Array[z, n]];

La meta es minimizar el potencial de Coulomb.

In[3]:=

potential = 
  Sum[((x[i] - x[j])^2 + (y[i] - y[j])^2 + (z[i] - z[j])^2)^-(1/
       2), {i, 1, n - 1}, {j, i + 1, n}];

Debido a que las partículas están en la esfera, sus coordenadas deben satisfacer restricciones de unidad de magnitud.

In[4]:=

sphereconstr = Table[x[i]^2 + y[i]^2 + z[i]^2 == 1, {i, 1, n}];

Seleccione puntos iniciales en la esfera al azar usando coordenadas esféricas.

In[5]:=

rpts = ConstantArray[1, n];
thetapts = RandomReal[{0, Pi}, n];
phipts = RandomReal[{-Pi, Pi}, n];
spherpts = Transpose[{rpts, thetapts, phipts}];

Transforme los puntos iniciales a coordenadas cartesianas.

In[6]:=

cartpts = CoordinateTransform["Spherical" -> "Cartesian", spherpts];

Reorganice los puntos iniciales para que coincidan con orden de variables.

In[7]:=

initpts = Flatten[Transpose[cartpts]];

Minimice el potencial de Coulomb sujeto a la restricción esférica.

In[8]:=

sol = FindMinimum[{potential, sphereconstr}, Thread[{vars, initpts}]];

Extraiga de la solución las posiciones de equilibrio de las partículas.

In[9]:=

solpts = Table[{x[i], y[i], z[i]}, {i, 1, n}] /. sol[[2]];

Represente gráficamente el resultado.

In[10]:=

Show[ListPointPlot3D[solpts, 
  PlotRange -> {{-1.1, 1.1}, {-1.1, 1.1}, {-1.1, 1.1}}, 
  PlotStyle -> {{PointSize[.03], Blue}}, AspectRatio -> 1, 
  BoxRatios -> 1, PlotLabel -> "Particle Distribution"], 
 Graphics3D[{Opacity[.5], Sphere[]}]]

Out[10]=