Solución de un problema de valor de límite usando la función de Green

Resuelva la siguiente ecuación diferencial de segundo orden sujeta a condiciones de límite homogéneas.

In[1]:=

eqn = -u''[x] - u'[x] + 6 u[x] == f[x];

In[2]:=

bc0 = u[0] == 0;

In[3]:=

bc1 = u[1] == 0;

El término de fuerza es dado por la siguiente función f[x].

In[4]:=

f[x_] := E^(-a x)

Calcule la función de Green para el operador diferencial correspondiente.

In[5]:=

gf[y_, x_] = GreenFunction[{eqn[[1]], bc0, bc1}, u[x], {x, 0, 1}, y]

Out[5]=

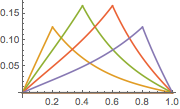
Represente gráficamente la función de Green para distintos valores de 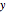que yacen entre 0 y 1.

In[6]:=

Plot[Table[gf[y, x], {y, 0, 1, 0.2}] // Evaluate, {x, 0, 1}]

Out[6]=

La solución de la ecuación diferencial original con el término de fuerza dado puede ahora ser calculado usando la integral de convolución en el intervalo .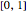

In[7]:=

sol = Integrate[gf[y, x] f[y], {y, 0, 1}, Assumptions -> 0 < x < 1] // Simplify

Out[7]=

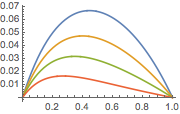
Represente gráficamente la solución para distintos valores del parámetro .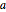

In[8]:=

Plot[Table[sol, {a, {1/4, 1, 2, 4}}] // Evaluate, {x, 0, 1}]

Out[8]=