Critério do círculo
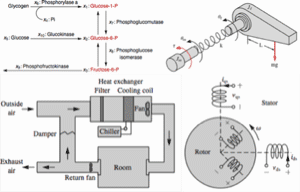
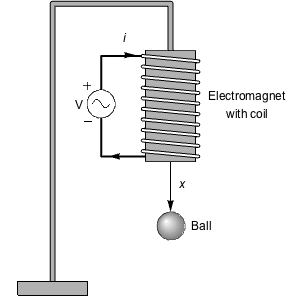
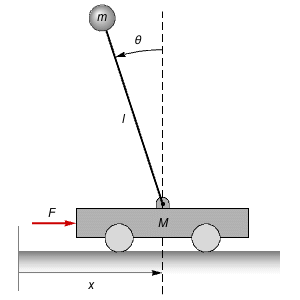
O problema de Lur'e investiga a estabilidade de uma importante classe de sistemas de controle cujo caminho adiante consiste de um sistema linear invariante no tempo e cujo caminho de realimentação consiste em uma não linearidade sem memória.
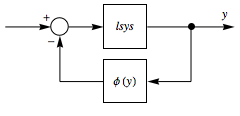 |
Para sistemas de entrada única e de saída única, o problema de Lur'e pode ser resolvido graficamente usando o critério do círculo. Ele postula que o número (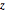 ) de pólos instáveis do sistema em malha fechada em que
) de pólos instáveis do sistema em malha fechada em que 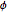 satisfaz a restrição do setor
satisfaz a restrição do setor 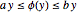 é dado por
é dado por 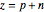 , onde
, onde 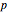 é o número de polos instáveis de
é o número de polos instáveis de 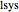 e
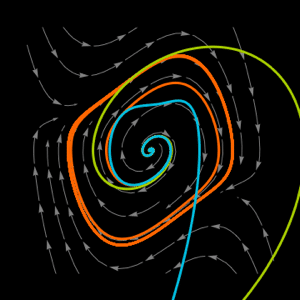
e  é o número de envolvimentos no sentido horário pelo gráfico de Nyquist de
é o número de envolvimentos no sentido horário pelo gráfico de Nyquist de 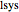 em torno do disco correspondente à realimentação no setor (
em torno do disco correspondente à realimentação no setor (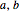 ).
).
Um sistema estável (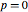 ).
).
| In[1]:= | X |
| In[2]:= | X |
| Out[2]= |
Para realimentação no setor (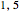 ), não há envolvimentos (
), não há envolvimentos (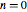 ).
).
| In[3]:= | X |
| Out[3]= | 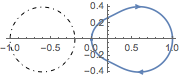 |
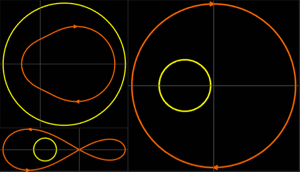
Várias não linearidades no setor de realimentação.
| In[4]:= | X |
| In[5]:= | X |
| Out[5]= | 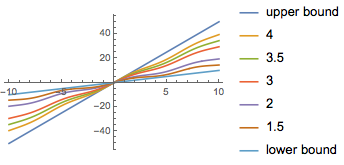 |
Simule o sistema de malha fechada estável (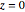 ).
).
| In[6]:= |  X |
| In[7]:= | X |
| Out[7]= | 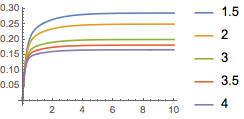 |