Criterio de círculo
El problema de Lur'e investiga la estabilidad de una clase importante de sistemas de control cuya trayectoria de avance consiste en un sistema lineal invariante en el tiempo y cuya trayectoria de retroacción consiste en una no linealidad sin memoria.
 |
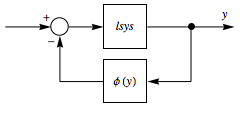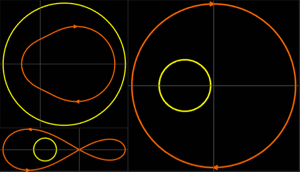
Para sistemas de una sola entrada o de una sola salida, el problema de Lur'e puede ser resuelto gráficamente usando el criterio de círculo. Este dice que el número (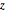
) de polos inestables de un sistema de circuito cerrado en el cual 
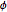satisface la restricción de sector 
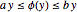es dada por 
, donde 
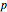es el número de polos inestables de 
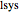y 
es el número de cercos hacia la derecha por el gráfico de Nyquist de 
alrededor del disco correspondiente a la retroacción en el sector (
).
Un sistema estable (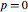
).
| In[1]:= |  X |
| In[2]:= |  X |
| Out[2]= |  |
Para retroacción en el sector (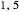
),no hay cercos (
).
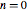| In[3]:= |  X |
| Out[3]= |  |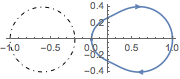
Varias no linealidades en el sector de la retroacción.
| In[4]:= |  X |
| In[5]:= |  X |
| Out[5]= |  |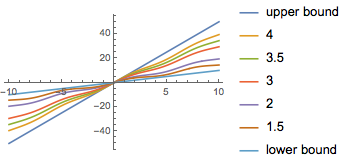
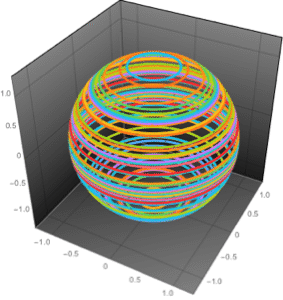
Simule el sistema estable de circuito cerrado (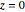
) .
| In[6]:= |  X |
| In[7]:= |  X |
| Out[7]= |  |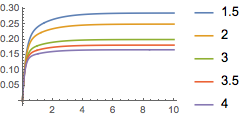
