Circle Criterion
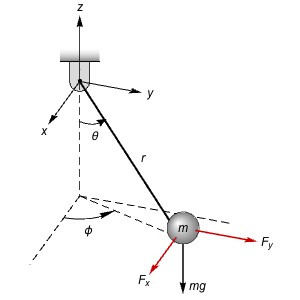
The Lur'e problem investigates the stability of an important class of control systems whose forward path consists of a linear time-invariant system and whose feedback path consists of a memoryless nonlinearity.
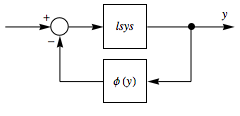 |
For single-input, single-output systems, Lur'e's problem can be solved graphically using the circle criterion. It says that the number (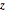 ) of unstable poles of the closed-loop system in which
) of unstable poles of the closed-loop system in which  satisfies the sector constraint
satisfies the sector constraint 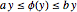 is given by
is given by  , where
, where 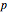 is the number of unstable poles of
is the number of unstable poles of  and
and  is the number of clockwise encirclements by the Nyquist plot of
is the number of clockwise encirclements by the Nyquist plot of  around the disk corresponding to the feedback in the sector (
around the disk corresponding to the feedback in the sector (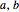 ).
).
A stable system ( ).
).
| In[1]:= | X |
| In[2]:= | X |
| Out[2]= |
For feedback in the sector ( ), there are no encirclements (
), there are no encirclements (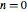 ).
).
| In[3]:= | X |
| Out[3]= | 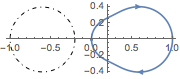 |
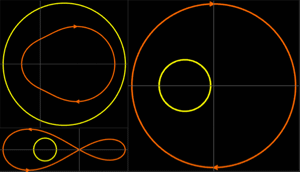
Various nonlinearities within the feedback sector.
| In[4]:= | X |
| In[5]:= | X |
| Out[5]= | 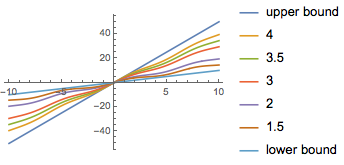 |
Simulate the stable ( ) closed-loop system.
) closed-loop system.
| In[6]:= |  X |
| In[7]:= | X |
| Out[7]= | 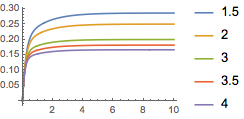 |