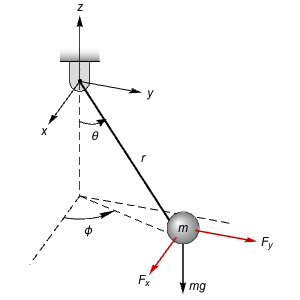
Construct a Nonlinear Estimator
Construct a nonlinear estimator using a predator-prey model to estimate the snowshoe hare population based on the lynx population. »
 |
The input to the model is and the output is ℓ.
| In[1]:= | X |
| In[2]:= | 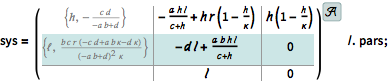 X |
The values of the initial population and a periodically varying food supply.
| In[3]:= | X |
The populations also vary periodically.
| In[4]:= | X |
| Out[4]= | 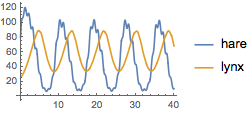 |
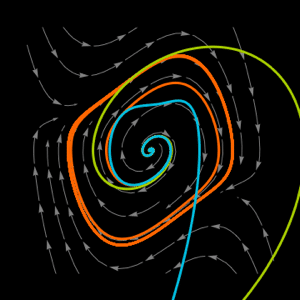
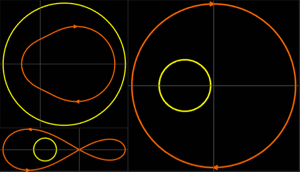
This limit-cycle behavior can also be seen on a parametric plot.
| In[5]:= | X |
| Out[5]= | 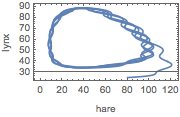 |
Compute a set of estimator gains based on the linearized model.
| In[6]:= | X |
| Out[6]= |
Construct the nonlinear estimator using the computed gains.
| In[7]:= | X |
| Out[7]= | 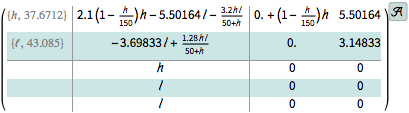 |
The observer inputs are and ℓ.
| In[8]:= | X |
| Out[8]= |  |
After initial transients, the estimated value converges to the actual one.
| In[9]:= | X |
| Out[9]= | 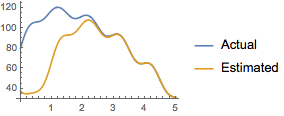 |