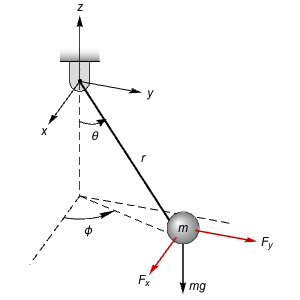
非線形推定器の構築
捕食者・被食者モデルを使って,オオヤマネコの個体数に基づいてカンジキウサギの個体数を推定するための非線形推定器を構築する. »
 |
モデルの入力は で,出力は ℓ である.
| In[1]:= | X |
| In[2]:= | 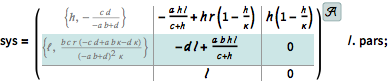 X |
初期個体数の値と定期的に変化する食物供給.
| In[3]:= | X |
個体数も定期的に変化する.
| In[4]:= | X |
| Out[4]= | 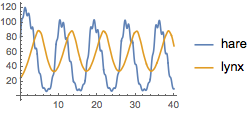 |
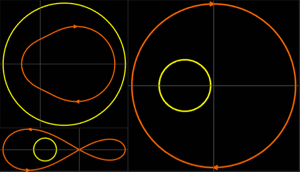
このリミットサイクル挙動はパラメトリックプット上でも見ることができる.
| In[5]:= | X |
| Out[5]= | 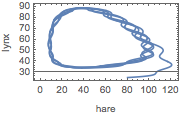 |
線形化されたモデルに基づく推定器ゲインの集合を計算する.
| In[6]:= | X |
| Out[6]= |
計算されたゲインを使って,非線形推定器を構築する.
| In[7]:= | X |
| Out[7]= | 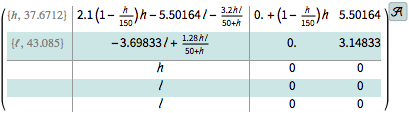 |
オブザーバ入力は と ℓ である.
| In[8]:= | X |
| Out[8]= |  |
初期トランジェントの後,推定された値は実際の値に収束する.
| In[9]:= | X |
| Out[9]= | 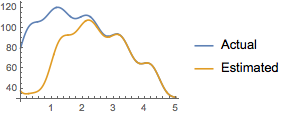 |