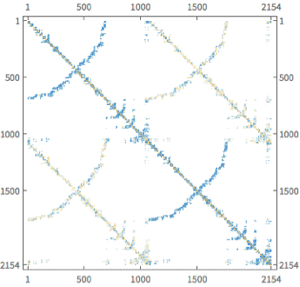
三次元の構造力学
固定されたクランク軸の，ピストンによりかかった負荷による変形を計算する．
Graphics3Dを指定する．
| In[1]:= |  X |
有限要素法パッケージをロードし，有限要素メッシュを生成する．
| In[2]:= |  X |
| Out[2]= |  |
三次元の応力を定式化する．
| In[3]:= | 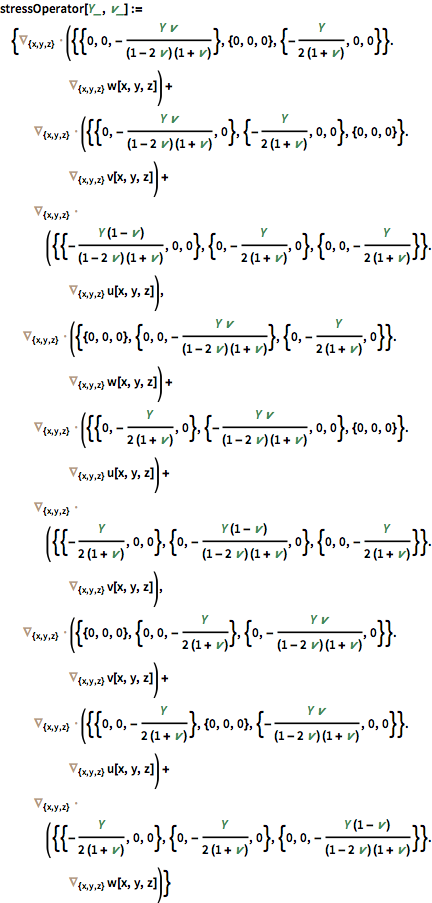 X |
クランク軸の境界が，これらの位置において固定されたままとなるような制約条件を指定する．
| In[4]:= |  X |
負の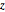 
軸に押し込む境界負荷を指定する．
| In[5]:= |  X |
連立方程式を解く．
| In[6]:= |  X |
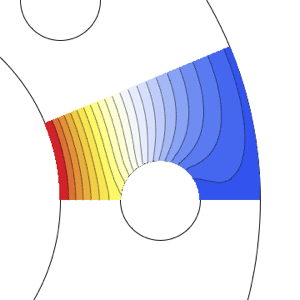
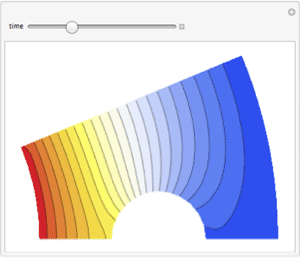
有限要素法パッケージを使って，もとのクランク軸と変形したクランク軸（赤）を可視化する．
| Out[7]= |  |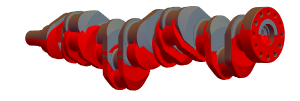
