Application Areas
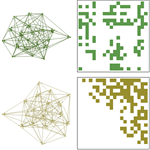
Graph & Network Analysis
Mathematica provides state-of-the-art functionality for analyzing and synthesizing graphs and networks. Building on Mathematica's powerful numerical and symbolic capabilities, Mathematica 8 brings numerous high-level functions for computing with graphs.
- Modern extensible platform for graph computation and network analysis. »
- Support for directed, undirected, and weighted graphs.
- Hundreds of built-in Mathematica functions and standard graph algorithms.
- Direct support for random graph distributions. »
- Extensive collection of graph operations and modifications. »
- Support for set-theoretic and Boolean-based operations on graphs. »
- Selection of graph elements and subgraphs using Mathematica pattern language.
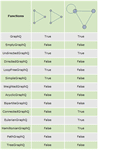
- Comprehensive collection of predicates for testing graph properties. »
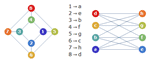
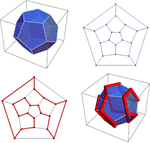
- Efficient graph isomorphism testing. »
- Local and global structural properties, including components, covers, and matchings.
- 15+ metrics and centrality measures to characterize graphs and networks. »
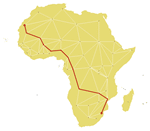
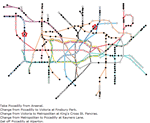
- Efficient shortest path, cycle, and navigation functions. »
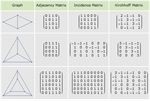
- Multi-paradigm approach to graph programming with matrix, optimization, and Boolean-based frameworks. »
- Generic BFS and DFS algorithms with a flexible programmatic interface. »
- Support of arbitrary properties for graph elements.
- Full integration of graphs and networks into Mathematica.