New and Improved Core Algorithms: New in Mathematica 8

Mathematica 8 adds a number of dramatic improvements to its core algorithms, with a new generation of methods for globally solving equations and inequalities, either symbolically or numerically. New symbolic-numeric methods allow you to numerically integrate a wide class of highly oscillatory functions automatically. Mathematica 8 reaches a new high-water mark in exact linear algebra performance, and also includes a number of additions to the world's largest collection of special functions.

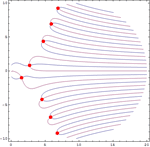
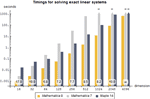
Solve can solve equations and inequalities over complexes, reals, and integers. »
NSolve can solve equations and inequalities over complexes and reals. »
Solve and NSolve have new advanced methods for solving transcendental equations.
Solve and NSolve have new advanced methods for finding real solutions to high-degree polynomials.
New conditionally valid expressions for representing partial functions. »
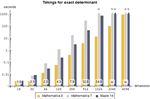
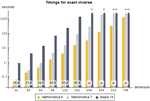
New generation of fast, exact linear algebra. »
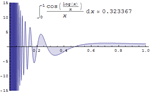
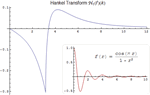
New hybrid symbolic-numeric method for integrating highly oscillatory functions. »
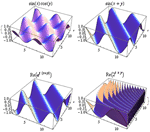
New special functions for probability and statistics. »


Compute with Conditionally Valid Solutions »	Find Parametrized Real Solutions of Systems of Equations »	Solve Transcendental Equations Numerically »

Solve High-Degree Real Polynomial Equations Numerically »	Conditionally Valid Expressions »	Fast Determinant Computation for Integer Matrices »

Fast Inverse Computation for Integer Matrices »	Fast Solving of Systems of Linear Equations with Integer Coefficients »	Fast Null Space Computation for Integer Matrices »

Solve a Numerical Integration Challenge Problem »	Integrate Sums, Products, and Compositions of Oscillatory Functions »	Integrate Multidimensional Highly Oscillatory Functions »

Compute Binormal Probability over a Polygon »	Sublevel Sets for RankedMin »	Eigenfunctions of the Laplace Equation »

Compute Values of High-Order Derivatives Directly »	Perform Numerical Hankel Transform »