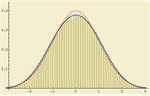
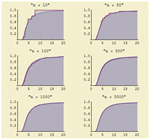
Building on two decades of development in symbolic and numeric algorithms, Mathematica 8 provides a suite of high-level functions for probability and statistics. New capabilities, including the ability to compute the probability of any event or the expectation of any expression, simulate any distribution, and automatically estimate parameters or test goodness of fit for distributions. To support distributional modeling and analysis, Mathematica 8 offers the largest collection of probability distributions, as well as full support for several dozens of properties, including distribution functions, moments, quantiles, and generating functions.

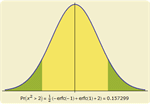
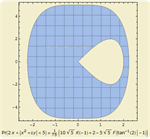
• Symbolic and numeric computation of probabilities and conditional probabilities of events as logical combinations of equations and inequalities. »
• Symbolic and numeric computation of expectations and conditional expectations of expressions. »
• Typeset characters for distributed (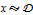) and conditioned (). »
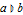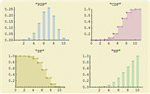
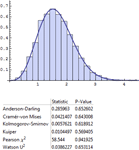
• Automatic support for simulating distributions, estimating parameters in distributions, and testing goodness-of-fit for distributions. »
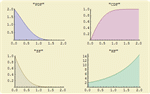
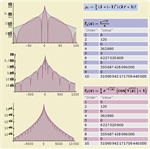
• Direct support for several different distribution functions including PDF, CDF, survival, hazard, inverse CDF, and inverse survival functions. »
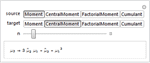
• Direct support for several different types of moments including raw moments, central moments, cumulants, and factorial moments. »
• Direct support for all the generating functions associated with moments, including moment-generating functions and cumulant-generating functions. »
• Automatic conversion from between different types of moments. »
• Automatic computation of standard and unbiased moment estimators. »

Compute the Probability of an Event »	Compute the Expectation of an Expression »	Compute Conditional Probabilities and Expectations »
Compute a Two-Tailed Probability  »	Lifetime of a Component »	Find the Expected Length of a Human Chromosome »
Find a Meeting Probability »	Univariate Continuous Distribution Functions »	Univariate Discrete Distribution Functions »
Bivariate Continuous Distribution Functions »	Bivariate Discrete Distribution Functions »	Perform an Edgeworth Expansion to Approximate a Distribution »
Demonstrate the Glivenko-Cantelli Theorem »	Compute a Complex Probability »	Study Dispersion and Location Measures »
Compare Two Distributions with the Same Moment Sequence »	Find a Closed Form for the Characteristic Function »	Find Multivariate Cumulants from Moments »
Construct Unbiased Estimators »	Convert between Formal Moments »	Find Expectations of Polynomials of Sample Estimators »
Estimate Parameters and Test Goodness of Fit »

RELATED FUNCTIONS

Probability  NProbability  Expectation  NExpectation  EstimatedDistribution  FindDistributionParameters  RandomVariate  DistributionFitTest  PDF  CDF  SurvivalFunction  HazardFunction  InverseCDF  InverseSurvivalFunction  Quantile  Moment  CentralMoment  FactorialMoment  Cumulant  MomentGeneratingFunction  CentralMomentGeneratingFunction  FactorialMomentGeneratingFunction  CumulantGeneratingFunction  MomentConvert  MomentEvaluate  Mean  Variance  StandardDeviation  Skewness  Kurtosis  Covariance  Correlation  Median