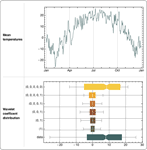
Application Areas
Wavelet Analysis
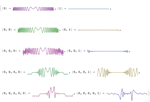
Mathematica 8 introduces a complete integrated wavelet analysis system, including a large collection of wavelet families and multiple variants of discrete wavelet transforms, as well as continuous wavelet transforms. Wavelet transforms are easy to use, with each transform producing a symbolic transform representation that makes it easy to access, manipulate, and visualize the tree of transform coefficients. Mathematica's new wavelet functionality also allows direct work on multidimensional data, sounds, and images without any conversion.
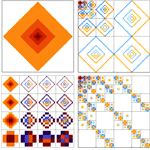
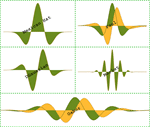
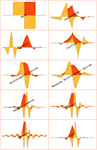
- Large collection of discrete and continuous wavelet families. »
- Scaling functions (
 ), wavelet functions (
), wavelet functions ( ), and filter coefficients for all wavelet families to arbitrary precision. »
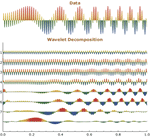
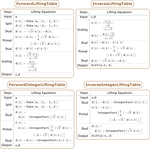
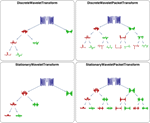
), and filter coefficients for all wavelet families to arbitrary precision. » - Discrete (DWT), stationary (SWT), and lifting wavelet transforms (LWT), including their inverses. »
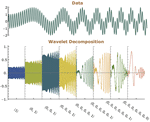
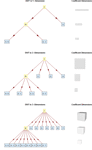
- Discrete (DWPT) and stationary wavelet packet transforms (SWPT), including best basis computation. »
- Compute discrete wavelet transforms for data of any number of dimensions. »
- Discrete transforms can directly operate on sound and images. »
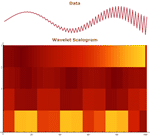
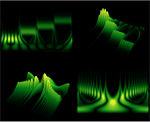
- Continuous wavelet transform (CWT), including inverse transform (ICWT). »
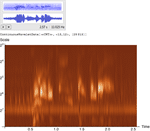
- Directly compute continuous wavelet transforms of sound. »
- Highly optimized performance and arbitrary-precision support for all transforms.
- All transforms produce symbolic wavelet decomposition that can be further manipulated. »
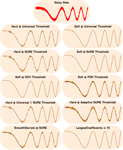
- Extensive support for wavelet thresholding methods. »
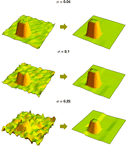
- Wavelet visualization functions, including scalogram and pyramid plots. »
/thumb_4.gif)
/thumb_5.gif)
/thumb_6.gif)
/thumb_7.gif)
/thumb_8.gif)

/thumb_12.gif)