Wolfram 语言™

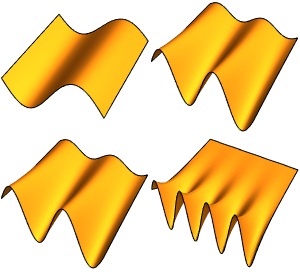
计算长方形上拉普拉斯算子的精确特征函数

设定齐次狄利克雷边界条件下的二维拉普拉斯算子.

In[1]:=

{\[ScriptCapitalL], \[ScriptCapitalB]} = {-Laplacian[u[x, y], {x, y}], DirichletCondition[u[x, y] == 0, True]};

求长方形内最小的四个特征值和特征函数.

In[2]:=

{vals, funs} = DEigensystem[{\[ScriptCapitalL], \[ScriptCapitalB]}, u[x, y], {x, 0, \[Pi]}, {y, 0, \[Pi]}, 4];

特征函数为三角函数.

In[3]:=

funs

Out[3]=

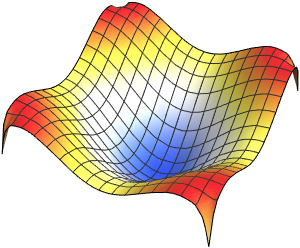
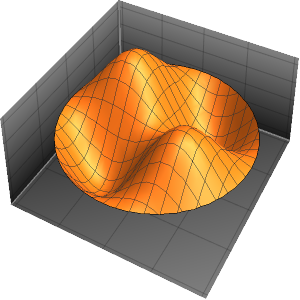
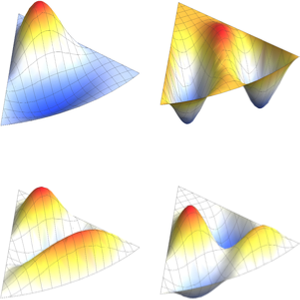
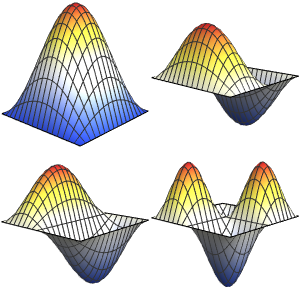
可视化特征函数.

In[4]:=

Plot3D[#, {x, 0, \[Pi]}, {y, 0, \[Pi]}] & /@ funs

Out[4]=